Распределение растений при пунктирном и гнездовом посевах
Одним из основных факторов, определяющих равномерность размещения растений по площади засеваемого поля, как известно, является исходная равномерность распределения семян. Однако для многих культур, в том числе и овощных, этот фактор не играет ведущей роли, так как действительное размещение растений значительно отличается от исходного распределения семян. Это обстоятельство обусловлено тем, что полевая всхожесть семян большинства овощных культур колеблется в пределах от 20 до 90%.
Отсюда становится очевидным, что чередование взошедших и не взошедших семян в рядке носит случайный характер. Следовательно, и расстояния между взошедшими семенами (расстояния между растениями) будут также величинами случайного порядка. Это дает основание при изучении процесса распределения растений использовать методы теории вероятностей и математической статистики.
Не задаваясь целью установить общие закономерности распределения интервалов между растениями, определим его числовые характеристики: математическое ожидание и дисперсию.
Чтобы упростить решение поставленной задачи, будем считать, что при односемянном (пунктирном) посеве семена располагаются с одинаковым интервалом и без пропусков, при гнездовом — с одинаковыми расстояниями между центрами гнезд и одинаковым без пропусков числом семян в гнезде.
Пусть произведен гнездовой посев по m штук семян в гнезде с расстоянием между гнездами 11П. Тогда, в силу независимости чередования всхожих и невсхожих семян, вероятность появления гнезд с различным числом растений может быть определена по формуле биномиального распределения:
Pn(m) - вероятность появления гнезд с числом растении n; P - вероятность появления одного растения из одного семени (полевая всхожесть в абсолютных единицах); q = 1 - Р — вероятность того, что из семени не появится растение; Сnm — сочетание из m по n.
Количество гнезд с тем или иным числом растений можно подсчитать по формуле
где 6 — число высеянных групп семян (число гнезд, образованных при посеве).
Общее число интервалов между растениями практически можно считать равным числу гнезд со всходами. Количество гнезд, где нет всходов, согласно выражению (6.2), равно
Следовательно, число гнезд cq всходами или интервалов между растениями
В соответствии с принятыми условиями, интервалы между гнездами, в которых появились всходы, могут быть равными lm, 2lm, 31m, — klm. Согласно уравнению (6.1), вероятность того, что всходы в гнезде не появятся, будет равна
Переходя к вероятности противоположного события, получим, что вероятность появления в гнезде хотя бы одного растения будет
Для образования интервалов между растениями при высеве семян группами необходимо и достаточно, чтобы в гнездах, находящихся друг от друга на расстоянии klm, было хотя бы по одному всхожему семени, т. е. по одному растению. Вероятность выполнения этого условия будет равна произведению вероятностей, выражаемых формулами (6.5) и (6.6). В соответствии с этим схема случаев образования интервалов величиной lm, 21т, 31т, ..., klm может быть представлена в следующем виде
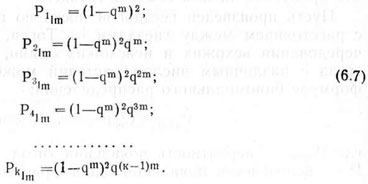
Ряд последовательности вероятностей (6.7), выражающих появление всходов через указанные интервалы, представляет собой геометрическую прогрессию со знаменателем qm, первым членом (a1) которой является выражение для P1lm, т. е. а1 = (1—qm)2. Но так ка 0<q<l последовательность, выражаемая (6.6), является бесконечно убывающей геометрической прогрессией, сумма которой равна
Для определения математического ожидания и дисперсии интервалов между растениями воспользуемся характеристической функцией случайной величины.
Характеристической функцией случайной величины X является 
где i — мнимая единица.
Функция f(t) представляет собой математическое ожидание некоторой комплексной случайной величины u = liU, функционально связанной с величиной X. Если случайная величина X дискретна, то ее характеристическая функция имеет вид
где Рк — вероятность (частота) появления случайной величины со значением х.
Для нашего случая характеристическая функция будет иметь вид
Подставив значения интервалов между растениями и соответствующих им частот, определяемых формулами (6.7) с учетом (6.12), в выражение (6.11), получим
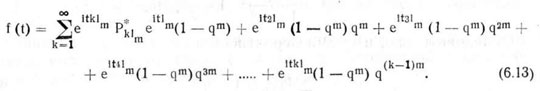
Первая производная от характеристической функции по t при t = 0 равна математическому ожиданию, умноженному на мнимую единицу i:
Подставив значение этой производной в формулу (6.16) и заменяя q = qm, получим выражение, отвечающее математическому ожиданию интервалов между растениями при гнездовом посеве
где l1 — значение интервала между семенами при односемянном посеве.
Дисперсия случайной величины lk, выраженной через характеристическую функцию, равна
Найдем вторую производную от характеристической функции распределения интервалов между растениями
Дифференцируя этот ряд по q, имеем
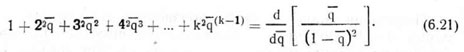
Следовательно, ряд, стоящий в квадратных скобках формулы (6.20), является производной по q выражения
Подставив значения f'(0) и f'(0) в формулу (6.19), получим [выражение для дисперсии интервалов между растениями при гнездовом посеве
Выражение для определения дисперсии интервалов между растениями при односемянном посеве находится из формулы (6.23), при m = 1
Если учесть, что при прочих равных условиях количество растений на единицу длины рядка принимается одинаковым, то исходные интервалы между семенами при односемянном и групповом посевах будут связаны следующим соотношением
Тогда с учетом этого соотношения формулы (6.17) и (6.23) примут вид
Выражения (6.25) и (6.26) получены в предположении постоянства интервалов между семенами. Если же это условие не соблюдается, то математические ожидания и дисперсии интервалов между растениями и семенами будут связаны следующими соотношениями:
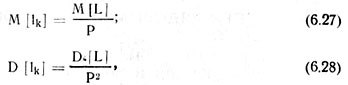
где М [L] и D[L] — математическое ожидание и дисперсия интервалов между семенами.
Расчеты по формуле (6.1) показывают, что односемянный посев эффективен только при полевой всхожести семян от 80 до 100%. При всхожести 65—80% предпочтение следует отдать размещению в гнезде по 2 семени, 45—65% — по 3 и 25—45% — по 4—6 семян. Это обеспечивает относительно малое число (процент) пустых гнезд и достаточно большое число гнезд с 1—2 растениями.
Из графиков (рис. 6.1 и 6.2), построенных по выражениям (6.25) и (6.26), видно, что математическое ожидание и дисперсия интервалов между растениями снижаются с увеличением полевой всхожести семян и уменьшением исходного интервала при посеве. Резкое снижение дисперсии с увеличением полевой всхожести особенно заметно при односемянном посеве. Увеличение семян в гнезде лишь незначительно уменьшает дисперсию интервалов между растениями.
При полевой всхожести семян, близкой к единице, математическое ожидание интервалов между растениями приближается к заданому интервалу и между семенами (или к математическому ожиданию исходных интервалов между семенами); дисперсия в этом случае приближается к нулю (или к дисперсии исходных интервалов между семенами).
Рис. 6.1. Зависимость математического ожидания интервалов между растениями от полевой всхожести и от числа их в гнезде.
Рис. 6.2. Зависимость дисперсии интервалов между растениями от полевой всхожести семян и от числа их в гнезде.
ДДоставка сельхозтехники и запасных частей, оросительных систем, насосов во все города России (быстрой почтой и транспортными компаниями), так же через дилерскую сеть: Москва, Владимир, Санкт-Петербург, Саранск, Калуга, Белгород, Брянск, Орел, Курск, Тамбов, Новосибирск, Челябинск, Томск, Омск, Екатеринбург, Ростов-на-Дону, Нижний Новгород, Уфа, Казань, Самара, Пермь, Хабаровск, Волгоград, Иркутск, Красноярск, Новокузнецк, Липецк, Башкирия, Ставрополь, Воронеж, Тюмень, Саратов, Уфа, Татарстан, Оренбург, Краснодар, Кемерово, Тольятти, Рязань, Ижевск, Пенза, Ульяновск, Набережные Челны, Ярославль, Астрахань, Барнаул, Владивосток, Грозный (Чечня), Тула, Крым, Севастополь, Симферополь, в страны СНГ:Киргизия, Казахстан, Узбекистан, Киргизстан, Туркменистан, Ташкент, Азербайджан, Таджикистан.
