Надежность комбинированных агрегатов
На современном этапе научно-технического прогресса в сельскохозяйственном машиностроении надежность является одним из основных факторов, определяющих эффективность использования машинно-тракторного парка и стоимость его эксплуатации. Подтверждением этого может служить тот факт, что затраты на ремонт и техническое обслуживание машин превышают в несколько раз их первоначальную балансовую стоимость. Из-за неисправностей в стране простаивает от 10 до 40% машин и оборудования, а ежегодные потери от этого составляют около 4 млрд. руб. [384].
Поэтому с ростом энерговооруженности сельского хозяйства, которое в основном будет осуществляться за счет поставок энергонасыщенных тракторов, новейших высокопроизводительных машин и комбинированных агрегатов, представляющих собой сложные системы, повышение надежности становится важнейшей не только технической, но и экономической задачей. От ее решения во многом будет зависеть дальнейший рост уровня механизации технологических процессов и повышение эффективности всего сельскохозяйственного производства в целом. В связи с этим вопросы надежности должны быть в центре внимания на всех этапах создания техники, начиная от разработки технического задания и проектирования и кончая испытаниями и промышленным производством.
Надежность — одно из совокупных свойств качества продукции — является объектом изучения теории надежности. Как инженерная дисциплина, теория надежности решает конкретные реальные задачи, выдвигаемые практикой. Основными ее методами являются теория вероятностей и математическая статистика. С помощью этих методов теория надежности устанавливает закономерности возникновения отказов и восстановления работоспособности изделий, рассматривает критерии и количественные характеристики надежности, определяет связь между ними, разрабатывает методы проведения испытаний на надежность, методы сбора, обработки и оценки опытной информации, устанавливает надежность машин и агрегатов в зависимости от надежности их узлов и деталей, определяет оптимальные показатели надежности и т. д. На этой основе представляется возможным наметить и осуществить конкретные мероприятия по дальнейшему совершенствованию конструкций, способов эксплуатации и ремонта машин.
Знание основ теории надежности и применение ее на всех стадиях создания машин будет в значительной мере способствовать достижению высокой эффективности использования техники, оборудования, материальных, финансовых и трудовых ресурсов, экономии топлива и энергии.
В данной главе рассматриваются физические и математические основы и количественные характеристики надежности комбинированных агрегатов, комплексов однооперационных и комбинированных машин, приводится расчет надежности овощного комбинированного агрегата.
Большая часть приводимых материалов в той или иной степени уже нашла отражение в действующей отраслевой нормативно-технической документации и широко используется в промышленности. Однако специфические особенности функционирования комбинированных агрегатов и отсутствие данных об их надежности вызвали необходимость в уточнении и детализации некоторых вопросов, касающихся расчета показателей надежности.
Зависимость основных характеристик надежности от действия определенного закона распределения
В теории надежности автоматических систем, различного рода машин и механизмов используется ряд законов распределения. Наибольшее распространение среди них получили нормальный, логарифмически нормальный, Пуассона, биномиальный, экспоненциальный, гамма-распределение, Релея, Вейбулла-Гнеденко и др.
Применительно к анализу надежности сельскохозяйственных машин в большинстве случаев используются законы нормального распределения, экспоненциальный и Вейбулла-Гнеденко [И, 5061.
Область применения того или другого закона распределения определяется видом и сложностью объекта (технического устройства), видом отказов, характером и причинами его возникновения.
Для анализа надежности сложных систем, прошедших соответствующий период приработки (обкатки), а также систем, работающих в тяжелых климатических условиях, под воздействием переменных динамических нагрузок, способствующих, как правило, появлению внезапных (случайных) отказов, в большей мере отвечает экспоненциальный закон распределения.
Нормальный закон распределения применяется для анализа систем, функционирующих в нормальных условиях, когда преобладают постепенные (износные) отказы. Если причинами отказовявляются усталостные повреждения, то показатели надежности с достаточной для практических целей точностью описываются логарифмически нормальным законом. При отказах, являющихся следствием совместного действия постепенных износов и усталостных повреждений, чаще других применяется распределение Вейбулла-Гнеденко. Последнее распределение дает достаточно хорошие результаты при анализе надежности большинства сельскохозяйственных машин [506].
Перечисленные законы распределения и указанные области
их применения с определенной идеализацией описывают физическую природу
отказов. Поэтому для каждого конкретного случая обоснованность избранного
теоретического распределения следует проверить опытом и с помощью специальных
математических приемов [506].
На практике при выборе закона распределения часто пользуются коэффициентом вариации, равным V = σ/M [384]. Если коэффициент вариации находится в пределах 0 ≤ V ≤ 0,30, то данные, полученные в результате опыта, соответствуют закону нормального распределения. При 0,3 ≤ V ≤ 0,8 распределение случайной величины может подчиняться как закону нормального распределения, так и закону Всйбулла-Гнеденко. В этом случае окончательный выбор закона распределения делается после уточнения данных по одному из наиболее точных критериев согласия [499].
Если дисперсия D[X] случайной величины равна ее математическому ожиданию, то экспериментальное (статистическое) распределение может с достаточной точностью аппроксимироваться распределением Пуассона.
При значениях коэффициента вариации 0,30 < V < l,0 может быть использован закон Вейбулла-Гнедснко, который при V = 0,52 и b = 2,0 (b — параметр закона распределения Вейбулла) переходит в закон Реллея.
Предпосылками возможности использования экспоненциального закона является равенство квадратического отклонения и математического ожидания, т. е. V = l.
Закон нормального распределения
Закон нормального распределения является двухпараметрическим и характеризуется плотностью вероятности вида
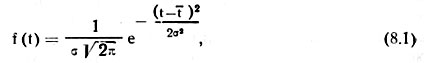
где t и σ — параметры распределения: математическое ожидание и квадратическое отклонение случайной величины. Вероятности отказа Q(t) и безотказной работы R(t) соответственно равны.
где t — значение заданного показателя надежности.
При расчете показателей надежности обычно используют центрированную функцию Fo(t) [5061.
Интенсивность отказов в общем случае определяется из отношения
Среднее время безотказной работы определяется как
Экспоненциальный закон распределения
Экспоненциальный закон распределения является однопараметрическим, а его плотность вероятности при х ≥ 0 имеет вид
где λ — параметр распределения {постоянная величина).
Зависимость между основными показателями надежности при этом законе распределения определяется уравнениями
Закон распределения Вейбулла-Гнеденко
Если вероятность безотказной работы описывается законом Вейбулла-Гнеденко, то зависимость между основными показателями надежности выражается уравнениями
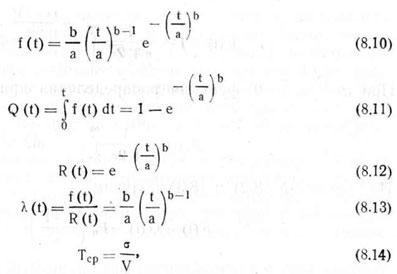
где а и b — параметры распределения Вейбулла-Гнеденко, определяемые на основании информации, полученной экспериментальным путем.
Для определения параметров а и b разработано несколько методов: по табулированным значениям в зависимости от коэффициента вариации V, метод максимального правдоподобия, графоаналитический и метод моментов. Из них наиболее точным является метод максимального правдоподобия, при котором параметр b определяется из уравнения
где N — число наблюденных значений случайной величины (число опытов); t1 — i-oe значение случайной величины.
Параметр b можно определить последовательным подбором его различных значений в интервале от 1,0 до 3,5, добиваясь равенства (8.15), или, что проще и менее трудоемко, графическим методом. Для этого, заменив через y1 левую, а через у2 правую часть уравнения (8.15) и подставляя в них не менее четырех значений b в том же интервале (1,0/3,5), строят график, по оси абсцисс которого откладывают значения b, а по оси ординат — значения y1 и у2. По полученным точкам (b1y1i и b1y2i) строятся кривые y1 и у2. Абсцисса точки пересечения этих кривых и является параметром b.
При известной величине параметра b параметр а определяется из уравнения
Из имеющихся законов распределения случайных величин приведены только те, которые в большей мере отражают физическую природу отказов и наиболее часто применяются при анализе надежности сельскохозяйственных машин. Сводная характеристика этих законов, их графическое изображение и область применения приведены в табл. 8.2. С другими законами распределения случайных величин можно ознакомиться в специальной литературе, и в частности в работе Я. Б. Шора [499].
Показатели надежности комбинированных агрегатов
В целом констатируя достигнутые успехи в создании и использовании сельскохозяйственных комбинированных агрегатов, следует отметить, что нередко фактическая производительность и другие технико-экономические показатели агрегатов оказываются значительно ниже расчетных и уступают аналогичным суммарным показателям соответствующих однооперационных машин, агрегатируемых раздельно. Одна из основных причин этого в том, что при разработке агрегатов комплектование их в большинстве случаев осуществлялось на основе совместимости выполнения технологических операций и энергетических возможностей трактора без должного учета надежности машин и орудий, включаемых в агрегат.
В последнее время опубликован ряд работ, в которых дается анализ влияния надежности комплектуемых машин и орудий на надежность и эффективность функционирования комбинированных агрегатов [336, 458]. Однако большинство из них посвящены агрегатам одноцелевого назначения, составленным из однотипных машин и орудий с одинаковым уровнем надежности, что, естественно, не позволяет использовать приведенные в них материалы при расчете надежности комбинированных агрегатов многоцелевого назначения, в составе которых имеются машины и орудия, различающиеся по надежности и другим технико-экономическим показателям.
Вероятностная модель комбинированного агрегата
Рассмотрим комбинированный агрегат (в дальнейшем для краткости агрегат) определенного целевого назначения, состоящий из разнотипных ремонтируемых машин и орудий, с различной надежностью, производительностью и другими технико-эксплуатационными показателями. При этом предполагается, что состав агрегата по тяговым и мощностным характеристикам соответствует техническим возможностям энергетического средства, а в функциональном отношении согласуется с совместимостью выполняемых им агротехнических операций.
Для сравнения данной модели агрегата естественно
принять комплекс машин (в дальнейшем — комплекс), предназначенный для выполнения той же цели и включающий те же однооперационные машины, агрегатируемые раздельно с соответствующими энергетическими средствами, рекомендуемыми заводами-изготовителями согласно нормативно-технической документации.
Таблица 8.2. Наиболее часто применяемые законы распределения.
В теоретическом и практическом отношении представляет интерес также сравнение комбинированного агрегата с комплексом, состоящим из двухоперационных машин (комбинированных машин), которые в настоящее время нашли широкое применение при возделывании многих сельскохозяйственных культур.
Особенностью функционирования рассматриваемых систем (комбинированного агрегата и сравниваемых комплексов) является то, что отказ одной из машин, входящих в агрегат, приводит к отказу в работе всего агрегата в целом, а отказ одной из машин комплекса не нарушает работу остальных. В реальных условиях эксплуатации последнее возможно тогда, когда машины комплекса работают параллельно, т. е. в разных загонах (участках), или же в том случае, когда для каждой из них заблаговременно выполняются предыдущие виды работ. При групповом (в одном загоне) методе работы однооперационных машин это условие нарушается и отказ одной из машин группы вызовет вынужденные простои следующих за ним тракторных агрегатов.
Таблица времени безотказной работы при оценке надежности сельскохозяйственных машин.
Естественно считать отказы машин в агрегате и комплексе независимыми, так как они есть следствие отказов входящих в них узлов и деталей, моменты появления которых являются независимыми случайными событиями.
применяя соответствующие положения теории вероятностей и теории надежности, а также учитывая действительный характер эксплуатации сельскохозяйственных машин, функционирование комбинированного агрегата, составленного по описанной выше схеме, может быть представлено математической (вероятностной) моделью в виде системы из последовательно соединенных восстанавливаемых элементов, отказ хотя бы одного из которых приводит к отказу всей системы в целом. В свою oчepeдь функционирование сравниваемого с агрегатом комплекса однооперационных машин может быть описано вероятностной моделью, представляющей собой систему из параллельно соединенных восстанавливаемых элементов, в которой отказ одного из них не нарушает работоспособность остальных. Сравниваемый комплекс комбинированных машин в данном случае может быть представлен системой из последовательно-параллельно соединенных элементов, в которой отказ элемента последовательной группы нарушает работоспособность только этой группы и не влияет на работу остальных. Предполагается, что отказы элементов являются независимыми, т. е. отказ любого из них никак не зависит от состояния любых других элементов.
Под элементом и здесь и в дальнейшем понимается машина, орудие или группа рабочих органов, выполняющих самостоятельную технологическую операцию.
Структурно-функциональная схема рассматриваемых систем показана на рис. 8.12.
Вероятность безотказной работы
Согласно принятым вероятностным моделям функционирования
рассматриваемых систем вероятность безотказной работы комбинированного агрегата
может быть определена как вероятность того, что за время t все элементы
системы будут работать безотказно, т. е. как вероятность совместного появления
независимых случайных событий (безотказности).
Рис. 8.12. Структурная схема функционирования комбинированного агрегата.
По теореме умножения вероятностей будем иметь
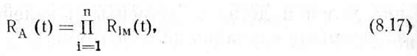
где RА(t) — вероятность безотказной работы комбинированного агрегата (системы с последовательным соединением элементов); Riм(t) — вероятность безотказной работы i-й машины агрегата (i-гo элемента системы).
Учитывая, что безотказная работа и отказ агрегата образуют полную группу и являются событиями несовместными и противоположными, вероятность отказа агрегата равна
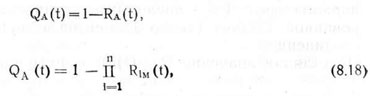
где QA(t) — вероятность отказа агрегата в течение времени t. Очевидно, что отказ комплекса из однооперационных машин (системы из параллельно соединенных элементов) возможен только тогда, когда откажут одновременно все машины и орудия (элементы системы) или когда отказы элементов возникнут в интервале времени восстановления одного из них. По теореме умножения вероятностей будем иметь
где QK(t) — вероятность отказа комплекса в течение времени t: Ом (t) — вероятность отказа i-й машины комплекса за время t; RK(t) — вероятность безотказной работы комплекса в течение времени t.
Для комплекса комбинированных машин (системы с последовательно-параллельным соединением элементов)* (см. рис. 8.12в) вероятность безотказной работы за фиксированный промежуток времени t равна
где Rnri — вероятность безотказной работы комбинированной машины (группы с последовательным соединением элементов); Ri(t) — вероятность безотказной работы i-й машины группы (i-гo элемента последовательной группы); m — число комбинированных машин (число последовательных групп, соединенных параллельно); к — число однооперационных машин в комбинированной машине (число элементов в группе с последовательным соединением).
Подставляя значение Rnri (t) в выражение (8.22), получим
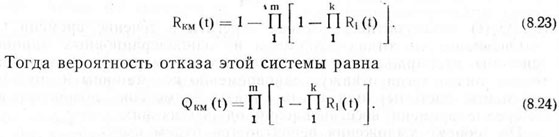
При равной надежности машин (элементов), входящих в агрегат и сравниваемые с ним комплексы, выражения для определения вероятности безотказной работы значительно упрощаются и принимают вид:
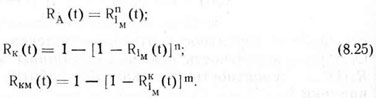
В реальных условиях эксплуатации фактические показатели надежности, и в частности вероятность безотказной работы сложных систем, значительно выше теоретических, полученных по расчетным формулам. Объясняется это идеализацией в законах распределения сроков службы машин и аппроксимацией их непрерывными распределениями [506]. При такой аппроксимации вероятность безотказной работы элементов системы начинает убывать сразу же после t = 0. Поэтому в этом случае даже при очень высокой надежности элементов (например, Ri(t)=0,99) система будет иметь низкое значение вероятности безотказной работы. Кроме того, принятые законы не учитывают изменений надежности элементов, обусловленных действиями периодических и ежесменных технических уходов и восстановлений, при проведении которых осматриваются и ремонтируются не только отказавшие узлы и детали, но и смежные (сопряженные) с ними, представляющие опасность возникновения отказов, что, естественно, повышает надежность этих элементов и системы в целом.
На самом же деле отказы элементов наступают не сразу после включения системы в работу, а по истечении некоторого периода. Оно и понятно, так как, исходя из физической природы отказов, трудно себе представить, чтобы детали и узлы машины были настолько некачественно изготовлены и смонтированы, что сразу же в начале работы исчерпают свои прочностные свойства и потеряют несущую способность. Если в этот период и наблюдаются отказы элементов, то они в абсолютном большинстве случаев обусловлены не столько отсутствием соответствующей надежности, сколько нарушением условий и правил эксплуатации машин (повышенная влажность почвы, низкое качество посевного или посадочного материала, технологических растворов жидкостей, заточки рабочих органов и т. д.).
В целях устранения имеющихся несоответствий между расчетными и фактическими показателями надежности предлагается некоторыми авторами [384, 506] при расчете вероятности безотказной работы сложных технических систем вводить для элементов зоны (участки) «нечувствительности», в которых R(t) = l. Тогда на участке (o,ti) (рис. 8.13) любое перемножение вероятностей безотказной работы элементов обеспечивает безотказность системы, равную единице.
Рис. 8.13. Кривые распределения R (t) и Q (t).
Величина зоны нечувствительности (o,ti) системы будет зависеть от наступления первого отказа самого ненадежного элемента. В нашем случае по комбинированному агрегату этот участок равен времени до первого отказа самой ненадежной его машины или орудия, а для сравниваемого комплекса — средней величине наработки до первого отказа машины, входящей в его состав.
В работах [377, 378] также указывается на несоответствие теоретических показателей надежности сельскохозяйственных машин, рассчитанных по формулам теории надежности, и фактических, определяемых по данным опытов. Для устранения этого несоответствия автором этих работ предлагается при расчете интенсивности отказов машины вместо среднего времени наработки на отказ (среднего времени безотказной работы) ввести время цикла работы, равного сумме времени безотказной работы и времени восстановления. Безусловно, это до некоторой степени уменьшает расхождение между расчетными и опытными показателями надежности, но противоречит самому понятию безотказности — свойству объекта непрерывно сохранять работоспособность в течение некоторого времени или некоторой наработки. Поэтому, как показывает анализ результатов испытаний, лучшее соответствие теоретических и фактических показателей надежности сложных систем обеспечивается, если при расчете интенсивности отказов элементов учитывать время (участок) нечувствительности, а не время восстановления.
Полученные зависимости (8.17), (8.21) и (8.23) показывают, что вероятность безотказной работы рассматриваемых систем зависит от надежности входящих в них элементов (машин) и структурной схемы их функционирования.
Одной из основных характеристик надежности ремонтируемых и перемонтируемых объектов является плотность распределения времени безотказной работы (плотность распределения наработки на отказ), которая в зависимости от вида отказа (внезапный или постепенный), характера и причин его возникновения описывается различными законами.
Отказы, возникаюшие при эксплуатации сельскохозяйственных машин, чаще всего носят внезапный характер, обусловленный наличием скрытых дефектов в узлах, деталях и их сопряжениях, нарушением рабочих режимов, забиванием и попаданием в рабочие органы машин посторонних предметов, приводящих к нарушению технологического процесса или поломкам, нечетким соблюдением технических условий по уходу и регулировкам, а также других рекомендаций как технического, так и эксплуатационного порядка. В результате этого моменты наступления отказов различаются между собой и образуют совокупность случайных величин (поток случайных событий — отказов) с определенной плотностью распределения.
В связи с этим функционирование каждого из элементов рассматриваемых систем в вероятностном смысле может быть описано случайным процессом, представляющим собой последовательность интервалов работоспособности, чередующихся с интервалами простоев (восстановлений), или же потоком случайных событий, параметрами которого являются интенсивности отказов и восстановлений. Тогда функционирование самих систем может быть представлено либо композицией случайных процессов, либо композицией (суммой) потоков случайных событий, обладающих определенными свойствами и распределениями.
Потоки отказов элементов рассматриваемых систем по своей физической сущности могут быть отнесены к числу простейших (пуассоновских), которые обладают свойствами ординарности, стационарности и отсутствия последействия.
Свойство ординарности в данном случае вытекает из пренебрежительно малой вероятности появления двух и более отказов элементов в один и тот же момент времени, а свойство стационарности обуславливается тем, что расчет надежности элементов систем, как правило, ведется для условий установившегося (стационарного) режима работы, т. е. для периода с началом сразу после приработки (тренировки) машин и до наступления отказов, вызванных износами и старением материалов узлов и деталей. Другими словами, для периода, когда процесс эксплуатации становится стабильным, а интенсивности отказов и восстановлений приобретают значения, близкие к постоянным.
Отсутствие последействия в потоке отказов элементов вытекает из того, что в нормальном установившемся (стационарном) режиме работы функционирование элементов после восстановления (ремонта) отказавших узлов и деталей не зависит от протекания процесса до их возникновения, т. е. после устранения отказа функционирование элементов начинается как бы заново и продолжается без снижения качества выполняемого процесса. Имеется в виду, что вероятность появления после ремонта того же отказа чрезвычайно мала.
Поэтому с достаточной для практических целей точностью поток отказов элементов (машин) можно отнести к простейшему с параметром, равным интенсивности отказов. Тогда, согласно предельной теореме Пальма [499], потоки отказов рассматриваемых нами систем (агрегата и комплексов) также будут простейшими с параметрами, равными сумме параметров суммирующих потоков.
Известно [499], что если поток случайных событий простейший, то промежутки времени между соседними событиями распределяются по экспоненциальному закону, параметр X которого равен параметру потока.
Применительно к рассматриваемому случаю это означает, что время безотказной работы (наработка на отказ) и время восстановления отказов элементов и в целом рассматриваемых систем — агрегата и комплексов — подчиняются одному и тому же экспоненциальному закону с функциями и плотностями распределения
где FР(t); FB(t) — функции распределения времени безотказной работы и времени восстановления; f (t); fB(l) — плотности распределения времени безотказной работы и времени восстановления; λ; μ — параметры законов распределения, а в нашем случае соответственно интенсивность отказов и интенсивность восстановлений.
Отличительной особенностью экспоненциального закона распределения безотказности и восстановления является независимость интенсивности отказов и восстановлений от времени, т. е. λ = const, μ = const.В реальных условиях эксплуатации это наблюдается только в период установившегося (нормального) режима работы, т. е. в период после приработки и до наступления износных и усталостных отказов. Поэтому в дальнейшем все показатели, характеризующие надежность рассматриваемых систем, будут определяться для нормального режима эксплуатации в предположении,, что соответствующие машины агрегата и комплексов имеют равную надежность.
Согласно экспоненциальному закону распределения, вероятность безотказной работы машины (элемента) в интервале времени от 0 до to равна:
где RiM(to) - вероятность того, что машина (элемент) проработает безотказно в течение заданного времени работы t0, начав работать в момент времени t = 0, или вероятность того, что время работы машины (элемента) до отказа окажется больше заданного времени работы t0.
Подставляя в (8.27) значение функции Fp(to), определяемое выражением (8.26), имеем
где λ1 — интенсивность отказов i-й машины агрегата и комплексов.
Учитывая условия, вытекающие из свойств простейшего потока и предельной теоремы Пальма, а также вероятность безотказной работы машины (элемента), определяемую выражением (8.28), найдем по уравнениям (8.17), (8.21) и (8.23) окончательные зависимости для определения вероятности безотказной работы комбинированного агрегата и сравниваемых с ним комплексов.Выражение для нахождения вероятности безотказной работы комбинированного агрегата, состоящего из п разнотипных машин, имеющих различную надежность, будет иметь следующий вид
Вероятность безотказной работы и вероятность отказа комплекса однооперационных машин при параллельном функционировании соответственно равны
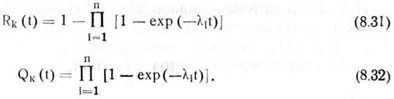
Вероятность безотказной работы и вероятность отказа комплекса комбинированных машин при параллельной работе (последовательно-параллельное соединение элементов)
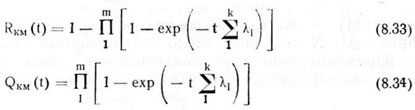
При одинаковой надежности машин выражения для определения вероятности безотказной работы рассматриваемых систем примут вид
Параметр потока отказов
В качестве характеристики потока отказов используется «ведущая функция» Q(t) данного потока — математическое ожидание числа отказов за время t
где r(t) — число отказов за время t.
Математическое ожидание числа отказов за интервал времени (t1, t2) определяется по формуле
где r(t1, t2) — число отказов за интервал (t1, t2).
Функция ω (t) называется интенсивностью потока отказов
Параметр потока отказов связан с ведущей функцией соотношением
По статистическим данным параметр потока определяется по отношению
где r (Δt) — число отказавших объектов (число отказов) за время Δt; N — общее число испытываемых объектов.
Применительно к рассматриваемым нами системам среднее значение параметра потока отказов равно
где ri(t), Тi — суммарное число отказов и наработка i-й машины агрегата (комплекса).
При экспоненциальном законе распределения времени безотказной работы параметр потока отказов равен интенсивности отказов
Интенсивность отказов в общем случае определяется отношением плотности распределения к вероятности безотказной работы
Подставляя значения величин, входящих в (8.37) согласно выражениям (8.26) и (8.29), найдем интенсивность отказов, а по (8.36) определим параметр потока отказов комбинированного агрегата
где λ1 — интенсивность отказов i-й машины агрегата (комплекса).
Следовательно, параметр потока отказов комбинированного агрегата при экспоненциальном законе безотказности равен сумме интенсивностей отказов машин, входящих в его состав.
Наработка на отказ
Наработка на отказ — среднее время наработки между отказами (без учета времени, затрачиваемого на восстановление) — при экспоненциальном распределении времени безотказной работы есть величина, обратная интенсивности отказов. Отсюда для каждой из машин рассматриваемых нами систем наработка на отказ равна
где То1 — наработка на отказ i-й машины, включая период (зону) нечувствительности. Тогда, согласно (8.38) и (8.39), наработка на отказ комбинированного агрегата равна
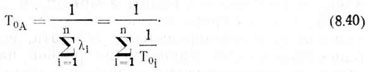
В данном случае в целях уменьшения несоответствия расчетных и фактических показателей надежности интенсивность отказов исчисляется с учетом зоны нечувствительности
где ТнА — зона нечувствительности (наработка до первого отказа агрегата).
По статистическим данным наработка на отказ агрегата определяется по формуле
где tj — время исправной работы агрегата между (i—1)-м и i-м отказами; r — число отказов за некоторое время t. Соответственно для сравниваемых комплексов наработка на отказ будет определяться по формулам
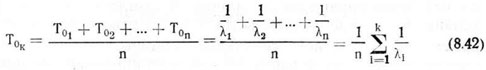
где Ток, Токм — наработка на отказ комплекса однооперационных и комбинированных машин; Т01r, Т02r, .... — средняя наработка на отказ i-й комбинированной машины; k — количество однооперационных машин в комбинированной машине (число машин в rpyппe); m — число комбинированных машин.
Легко заметить, что при m = 1 и k = n выражение (8.43) переходит в выражение (8.40), а при m = n и к = 1 в выражение (8.42), т. с. в первом случае это будет соответствовать функционированию комбинированного агрегата, во втором — комплекса однооперацнонных машин. При равной надежности машин, входящих в рассматриваемые системы, выражения (8.40), (8.42) и (8.43) примут соответственно вид
Средняя наработка до отказа
Средняя наработка до отказа агрегата равна наработке до первого отказа самой ненадежной машины
Средняя наработка до отказа сравниваемых комплексов определяется по формулам
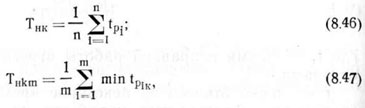
где TиА, Tим и Тикм — средняя наработка до отказа агрегата, комплекса однооперационных машин и комлекса комбинированных машин; tp, — время работы до первого отказа i-й машины; tPlk — время работы до первого отказа машины, входящей в группу (время работы до первого отказа комбинированной машины).
Интенсивность восстановления
Интенсивность восстановления элемента (машины) при экспоненциальном законе распределения времени восстановления, так же как и интенсивность отказов, является величиной постоянной
где fb(t) — плотность распределения времени восстановления; Rb(t) — вероятность восстановления в заданное время или вероятность того, что время восстановления системы не превысит заданного.
Среднее время восстановления
Среднее время восстановления — математическое ожидание времени восстановления — при экспоненциальном законе распределения равно обратной величине интенсивности восстановления
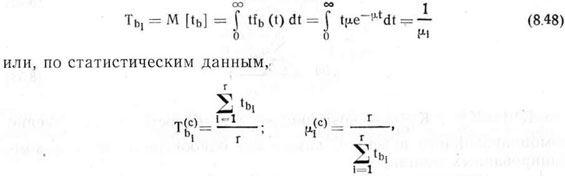
где tbi — время, затраченное на восстановление i-гo отказа, включая время поиска причин отказа.
Учитывая принятые условия о том, что рассматриваемые системы (агрегат и комплексы) состоят из одинакового количества соответственно равнонадежных машин, и предполагая, что время восстановления каждой из них является независимыми случайными величинами и не пересекаются, т. е. вероятность восстановления двух и более элементов в один и тот же момент времени пренебрежительно мала, среднее время восстановления каждой из систем равно
где μi — интенсивность восстановления i-й машины агрегата и комплекса.
Коэффициент готовности
По статистическим данным коэффициент готовности в общем виде определяется по формуле
где t01 — суммарное время исправной работы 1-го объекта за фиксированный промежуток эксплуатации; Т — суммарное время эксплуатации, состоящее из последовательно чередующихся интервалов времени работы и восстановления; N — число объектов, находящихся на испытании.
Для рассматриваемых нами систем формула (8.50) примет вид
где 
— коэффициенты готовности соответственно комбинированного агрегата, комплекса однооперационных и комбинированных машин; toA — суммарное время исправной работы комбинированного агрегата; toki —суммарное время исправной работы i-й однооперационной машины комплекса; tck j — суммарное время исправной работы i-й комбинированной машины комплекса; Та, Тк, Ткм — суммарное время исправной работы и восстановления соответственно комбинированного агрегата, комплекса однооперационных и комбинированных машин; n; m — число однооперационных и комбинированных машин. В установившемся режиме работы коэффициент готовности объекта в общем виде определяется по формуле
где То — наработка объекта на отказ; Тb — среднее время восстановления.
Подставляя в выражение (8.54) значение входящих в него величин, согласно (8.40), (8.42), (8.43) и (8.49), определим коэффициент готовности рассматриваемых систем
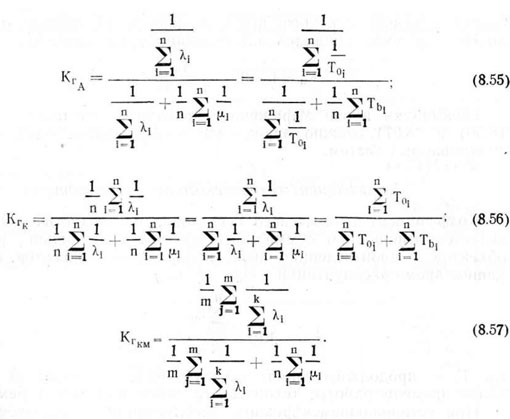
При равной надежности машин, входящих в агрегат и сравниваемые комплексы, выражения для коэффициента готовности примут вид
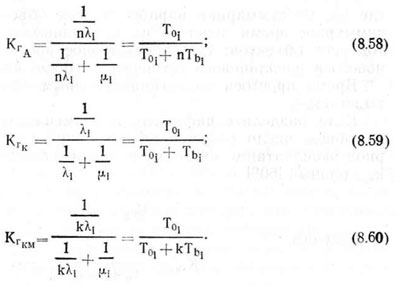
Из этих выражений видно, что наибольшим коэффициентом готовности обладает комплекс, состоящий из однооперационных машин. При этом коэффициент готовности комплекса равен коэффициенту готовности машины.
По аналогии с отказом и безотказностью для оценки машин и систем используется показатель — коэффициент простоя. Он означает вероятность того, что в произвольный момент времени объект (система) окажется в состоянии отказа (восстановления)
Подставляя в это выражение значения кг согласно (8.55), (8.56) и (8.57), можно определить коэффициенты простоя рассматриваемых систем.
Коэффициент технического использования
Коэффициент технического использования статистически определяется отношением суммарного времени исправной работы объектов к произведению числа наблюдаемых объектов на заданное время эксплуатации
где Тэ — продолжительность эксплуатации, состоящей из интервалов времени работы, технического обслуживания и ремонтов. При установившемся режиме эксплуатации коэффициент технического использования определяется по формуле
где tсyм — суммарная наработка всех объектов системы; tpeм — суммарное время простоев из-за плановых и внеплановых ремонтов всех объектов; tl>Qc — суммарное время простоев из-за планового и внепланового технического обслуживания всех объектов.
Время простоев по организационным причинам здесь не учитывается.
Если разделить числитель и знаменатель выражения (8.63) на общее число отказов, возникающих за рассматриваемый период эксплуатации системы, и ввести коэффициент профилактики кпр, равный
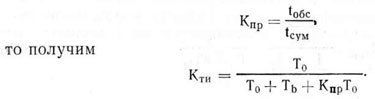
Разделив числитель и знаменатель этого выражения на То, будем иметь
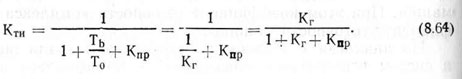
Выражение (8.64) отражает взаимосвязь коэффициентов готовности и технического использования ремонтируемого объекта (системы). Подставляя в него значения к,, определяемые выражениями (8.55), (8.56) и (8.57), получим формулы для определения коэффициентов технического использования соответственно комбинированного агрегата, комплексов однооперационных и комбинированных машин. Расчетные формулы для показателей надежности рассматриваемых систем при экспоненциальном законе распределения времени безотказной работы приведены в табл. 8.3.
Анализ полученных зависимостей для определения показателей надежности рассматриваемых систем позволяет сделать следующие выводы:
Безотказность комбинированного агрегата и комплексов однооперационных и комбинированных машин зависит от безотказности и количества входящих в них машин. При этом с повышением безотказности машин безотказность агрегата и комплексов увеличивается.
Комбинированный агрегат по надежности значительно уступает комплексу однооперационных машин и несколько меньше — комплексу комбинированных машин при параллельном их функционировании.
С увеличением числа машин в комбинированном агрегате безотказность его резко падает даже при достаточно высокой вероятности безотказной работы каждой машины, входящей в его состав.
В целях обеспечения достаточной надежности комбинированного агрегата в его состав следует включать оптимальное количество машин, обладающих высоким уровнем надежности.
Полученные аналитические зависимости для определения единичных и комплексных показателей надежности могут быть использованы при расчете на стадии комплектования и проектирования комбинированных агрегатов, а также при технико-эксплуатационной оценке их в процессе испытаний.
ДДоставка сельхозтехники и запасных частей, оросительных систем, насосов во все города России (быстрой почтой и транспортными компаниями), так же через дилерскую сеть: Москва, Владимир, Санкт-Петербург, Саранск, Калуга, Белгород, Брянск, Орел, Курск, Тамбов, Новосибирск, Челябинск, Томск, Омск, Екатеринбург, Ростов-на-Дону, Нижний Новгород, Уфа, Казань, Самара, Пермь, Хабаровск, Волгоград, Иркутск, Красноярск, Новокузнецк, Липецк, Башкирия, Ставрополь, Воронеж, Тюмень, Саратов, Уфа, Татарстан, Оренбург, Краснодар, Кемерово, Тольятти, Рязань, Ижевск, Пенза, Ульяновск, Набережные Челны, Ярославль, Астрахань, Барнаул, Владивосток, Грозный (Чечня), Тула, Крым, Севастополь, Симферополь, в страны СНГ:Киргизия, Казахстан, Узбекистан, Киргизстан, Туркменистан, Ташкент, Азербайджан, Таджикистан.
