Распределение семян сеялками точного высева
Основной задачей посева является внесение семян в почву и заделка их на заданную глубину. В зависимости от способа посева эта задача конкретизируется требованиями распределения семян по площади засеваемого поля. В частности, для рядового посева с пунктирным и гнездовым размещением семян такими требованиями являются, соответственно, равномерность распределения интервалов между семенами в ряду и равномерность распределения интервалов между гнездами семян. В последнем случае добавляется еще требование по количеству и компактности размещения семян в гнезде.
Следовательно, основными показателями качества работы сеялок точного высева, т. е. выходными оценочными критериями выполняемого ими технологического процесса (выходными переменными), служат равномерность распределения интервалов между семенами в рядке и равномерность глубины заделки семян.
В соответствии с агротехническими требованиями на овощные сеялки точного высева [4] указанные показатели качества оцениваются числовыми характеристиками распределений интервалов между семенами и глубины заделки семян: средним арифметическим, средне-квадратическим отклонением (дисперсией) и коэффициентом вариации.
Анализ технологического процесса работы посевных машин и опыт их эксплуатации показывают, что основными внешними возмущающими воздействиями (входными факторами), оказывающими влияние на распределение семян, являются профиль поверхности поля, твердость и влажность почвы, скорость движения агрегата, нестабильность работы двигателя, буксование колестрактора и другие. В соответствии с внутренней структурой высевающих систем на распределение интервалов между семенами значительное действие оказывают неравномерность подачи семян высевающими аппаратами, обусловленная колебаниями скорости вращения их высевных устройств, изменчивость параметров движения семян в семяпроводе, сошнике и по дну раскрытой им борозды. Иначе говоря, при нормальном функционировании посевной мащины выходные показатели технологического процесса зависят не только от внешних воздействий, но и от внутренней структуры высевающих систем.
Вследствие специфических особенностей работы почвообрабатывающих машин, природных свойств почвы и влияния окружающей среды внешние входные воздействия в процессе движения (работы) посевного агрегата непрерывно изменяются, в результате чего на агрегат фактически действуют случайные факторы, совокупность которых во времени образует случайные процессы (случайные функции). Соответственно этому внутренние факторы и выходные параметры (показатели) технологического процесса посева, как результаты действия преобразующей системы (посевной машины), также будут случайными функциями.
Рис. 4.2. Структурная схема функционирования сеялки точного высева.
Рис. 4.3. Структурная схема функционирования высевающей системы сеялки точного высева (а); и процесса заделки семян сеялками точного высева (б).
Исходя из указанных предпосылок сеялку точного высева в общем случае можно представить в виде многомерной динамической системы (рис. 4.2), на вход которой поступают внешние воздействия (случайные функции) от профиля поля Z(L), твердости и влажности почвы, соответственно p(L) и W(L), скорости движения агрегата V(L), буксования колес трактора e(L) и нестабильности работы двигателя N(L); внутренние воздействия от высевающего аппарата То(п), семяпровода Т(к), сошника Тс (к), профиля борозды Hn(fx), заделывающих устройств H(iL) и колебания рамы сеялки K(L). Выходом системы будут равномерность распределения интервалов между семенами (гнездами) 1(L) и глубина заделки семян h(L).
Из приведенной структурной схемы, в которой, кстати сказать, не учтены еще управляющие и задающие воздействия, видно, что построение математической модели функционирования сеялки точного высева методом идентификации представляет чрезмерные трудности как экспериментального, так и вычислительного порядка, если даже принять для упрощения систему линейной и воспользоваться ее свойством суперпозиции. Однако следует подчеркнуть, что решение этой задачи методами механики практически не представляется возможным. Поэтому применение механико-статистических (комбинированных) методов построения математических моделей указанной и подобных ей систем, как будет показано ниже, значительно упрощает решение задачи и обеспечивает достаточную для практических целей точность получаемых результатов.
Характер и последовательность протекания технологического процесса посева, а также внутренняя структура и функциональные особенности рабочих органов позволяют расчленить общую структурную схему функционирования сеялок точного высева (см. рис. 4.2) на две самостоятельные схемы (динамические модели), одна из которых будет отражать работу высевающей системы — процесс распределения семян вдоль рядка, другая — по глубине заделки. Правомерность такого расчленения вытекает из независимости (вернее, слабой зависимости) этих процессов и их выходных параметров. Процесс распределения семян вдоль рядка в этом случае может быть представлен динамической моделью (рис. 4.3а), состоящей из трех взаимосвязанных последовательно соединенных частей, основным входом в которую является комплексный (интегральный) показатель Q(L) внешних возмущающих воздействий, а входами и выходами отдельных частей служат обороты (скорость вращения) опорно-приводных колес сеялки T„(Q), время между выбрасыванием семян высевающим аппаратом To(t„), комплексный показатель физико-механических свойств высеваемых семян Т(0)и профиль борозды, раскрытой сошником H„(fx). Общим выходом модели является равномерность распределения интервалов между семенами (гнездами) в рядке 1(L).
Замена внешних воздействий в данном случае одним интегральным показателем обусловлена, во-первых, тем, что все внешние воздействия свое влияние на выходные показатели системы оказывают через ее первую и вторую части, т. е. через обороты приводных колес сеялки и время между выбрасыванием семян, во-вторых, — техническими трудностями в синхронной записи входных и выходных случайных функций, в третьих, — возможностью сокращения объема экспериментальных и вычислительных работ.
Такая постановка вопроса, разумеется, не исключает возможности анализа поведения системы в зависимости от каждого внешнего воздействия, но она позволяет значительно упростить решение задачи без снижения точности получаемых результатов.
Структурная схема процесса заделки семян в почву (распределения семян по глубине) показана на рис. 4.36. Входными переменными в этой динамической системе приняты профиль поля Z(L) и твердость почвы p(L) как факторы, оказывающие основное влияние на работу сошниковой группы; внутренними воздействиями — колебания рамы сеялки K(L), заделываюнще и прикатывающие устройства H(L); выходной переменной — равномерность глубины заделки семян h(L).
Распределение семян вдоль рядка
Технологический процесс распределения семян вдоль рядка у большинства овощных и других сеялок точного высева состоит в следующем. Семена из бункера под собственным весом (самотеком) поступают в заборную камеру высевающего аппарата. Высевающее устройство аппарата захватывает из заборной камеры заданное количество семян, транспортирует их и через определенные промежутки времени сбрасывает в семяпровод, откуда они попадают в раскрытую сошником борозду и располагаются в ней на некотором расстоянии друг от друга. В некоторых конструкциях сеялок семяпроводы как таковые отсутствуют и семена сбрасываются либо непосредственно в борозду, либо на специальные скатные поверхности, размещаемые в полости сошника, с которых они затем падают в борозду.
Привод высевающих аппаратов в современных овощных сеялках точного высева секционного исполнения, как правило, осуществляется от опорных колес сеялки через многоступенчатые коробки перемены передач. Поэтому промежуток времени между выбрасыванием семян высевающим аппаратом находится в определенной функциональной зависимости от скорости вращения приводного колеса сеялки, которая выражается уравнением 
(4.12) или с учетом скольжения приводных колес где t0 — промежуток времени между выбрасыванием семян высевающим аппаратом, с; t — время одного оборота приводного колеса сеялки, с; ts — время одного оборота холостого колеса сеялки (время одного оборота колеса сеялки при отсутствии скольжения), с; i — передаточное отношение между оборотами колеса сеялки и высевающим аппаратом; Z — число порций семян, высеваемых аппаратом за один оборот (число присасывающих отверстий или ячеек на высевающем устройстве аппарата); е — коэффициент скольжения приводного колеса сеялки.
Как уже отмечалось, в результате воздействия ряда внешних случайных факторов скорость вращения приводных колес сеялки или, что то же самое, время одного оборота колеса и коэффициент скольжения их (выходной параметр первой части системы и входной — второй) носят случайный характер. Следовательно, промежуток времени (to) между выбрасыванием семян высевающим аппаратом является функцией непрерывно меняющихся аргументов (t,;, б), т. е. также является случайной функцией [То (t„, е)].
Время падения семян от высевающего аппарата до дна борозды также является случайной величиной, что обусловлено значительной изменчивостью физико-механических свойств семян.
Однако в процессе движения семян от высевающего аппарата до дна борозды наблюдаются не только случайные, но и вполне закономерные факторы. В частности, в высевающих системах при вертикальной установке семяпроводов или без них основная масса семян практически достигает дна борозды в условиях свободного падения; движение в наклонном семяпроводе или по скатным поверхностям эквивалентно движению тела с трением и сопротивлением среды по наклонной плоскости. Следовательно, процесс движения каждого отдельного семени может быть описан методами классической механики. Такой подход, так же как и на этапе транспортирования (подачи) семян высевающим устройством, не отрицает случайного характера процесса в целом, но позволяет установить функциональную зависимость между его параметрами, определить вид случайной функции, характеризующей данный процесс, и, в итоге, значительно облегчает построение оператора (математической модели) этой системы.
Найдем аналитическую зависимость между параметрами наиболее часто встречающихся видов движения семян от высевающего аппарата до дна раскрытой сошником борозды.
В современных овощных сеялках при транспортировании семян от высевающего аппарата до дна борозды по семяпроводам движение семян, в зависимости от конструкции и установки семяпровода, может происходить в условиях свободного падения с начальной скоростью, близкой к нулю (вертикально установленные семяпроводы), и со скольжением по шероховатой поверхности с некоторой начальной скоростью (наклонные семяпроводы). При подаче семян аппаратом непосредственно в борозду в большинстве случаев происходит свободное падение с начальной скоростью, примерно равной линейной скорости вращения высевающего устройства аппарата. Рассмотрим указанные виды движения семян в отдельности.
Предположим, что свободное падение основной массы семян в вертикально установленном семяпроводе является движением изолированных одна от другой частиц. Тогда в первом приближении для анализа этого движения можно применить принципы динамики материальной точки, рассматривая при этом падение семени как поступательное движение, а само семя — как материальную точку с массой т.
Рис. 4.4. К определению параметров движения семян при свободном падении в вертикальном семяпроводе.
Совместим начало координат 0 с начальным положением движущейся точки и направим вертикальную ось вниз (рис. 4.4). На движущуюся точку в этом случае будут действовать две силы: сила тяжести Q = mg, направленная по вертикали вниз, и сила сопротивления воздуха R, направленная вертикально вверх.
Сила сопротивления воздуха зависит от скорости движения тела. При скоростях, больших 0,2 м/с, силу сопротивления воздуха обычно считают пропорциональной второй степени скорости (v): R = KV2, где К — коэффициент сопротивления.
Составим дифференциальное уравнение движения точки или для нашего случая
или для нашего случая
После подстановки значений Q и R и сокращения на массу, получим
(4.13)
Если в уравнение (4.13) ввести скорость витания (парусность) семян Vкp, значение которой равно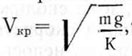 
, то оно примет вид
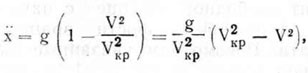
или
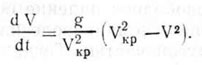(4.14)
Выражение (4.14) является дифференциальным уравнением первого порядка с разделяющими переменными, разделяя которые, получим
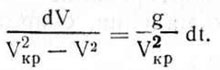
Интегрирование этого уравнения при начальных условиях t = 0, х = 0, V0 = 0 и некоторые преобразования его дают возможность установить параметры движения семян при свободном падении их с некоторой высоты h.
Зависимость (4.17) для удобства анализа изображена графически (рис. 4.5). При постоянстве высоты падения семян, т. е. высоты расположения высевающего устройства над поверхностью дна борозды, время свободного падения семян полностью и однозначно определяется их скоростью витания. При этом с увеличением скорости витания время падения семян уменьшается, что особенно заметно в диапазоне высот от 0,6 м и выше. При высоте падения до 0,15 м скорость витания практически не влияет на время падения семян. Из этого следует, что при расчете и проектировании высевающих систем, дозирующие устройства (точки сбрасывания семян) которых располагаются на высоте до 0,15 м от дна борозды, а транспортирование семян происходит путем вертикального свободного падения, сопротивление воздуха можно не учитывать.
Рис. 4.5. График зависимости времени движения семян в вертикальном семяпроводе.
Рис. 4.6. К определению параметров движения семян по наклонному семяпроводу.
Движение семян по наклонному семяпроводу (рис. 4.6) в общем случае описывается уравнениями.
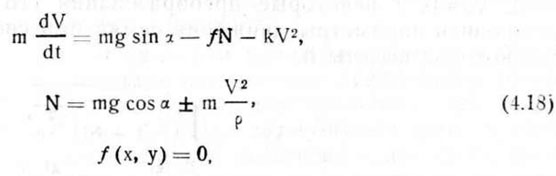
где f (x, y) = 0 — уравнение кривой, в плоскости которой перемещается частица (уравнение связи); N — нормальная реакция; f — коэффициент внешнего трения семян; a — угол наклона семяпровода (текущее значение); р — радиус кривизны семяпровода (кривой) (знак «+» относится к кривой вогнутой формы, знак «—» — к выпуклой).
Исключив из первых двух уравнений (4.18) нормальную реакцию, получим
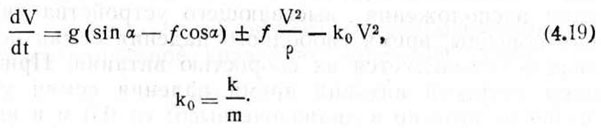
Но, учитывая, что
или
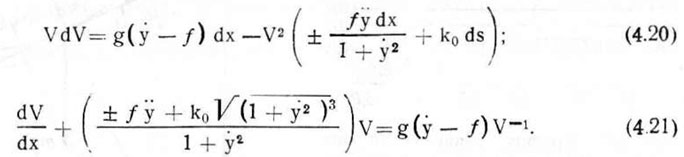
Введя обозначения
Выражение (4.23) является дифференциальным уравнением типа Бернулли с коэффициентами Р(х) и Q(.\). Его решением является интеграл
где С — произвольная постоянная.
При заданном уравнении связи (уравнении кривой, в плоскости которой перемещается семя) задача определения параметров движения единичных семян решается до конца. Действительно, из уравнения (4.24) находим x = f(V), а по уравнению связи f(x, у) =0 — пройденный семенем путь S в функции от х, т. е. S = f2(x). Тогда из этих уравнений определяется пройденный путь в функции скорости - S = f3(V) и обратно V = ?4(S) и, наконец, из уравнения V = f4(S) находится выражение для установления времени движения семени в зависимости от пройденного им пути.
Итак, при транспортировании семян от высевающего аппаратг. до дна борозды по прямому наклонному семяпроводу (по наклонной прямой) решение указанных выше уравнений дает следующие выражения для определения параметров движения единичных семян
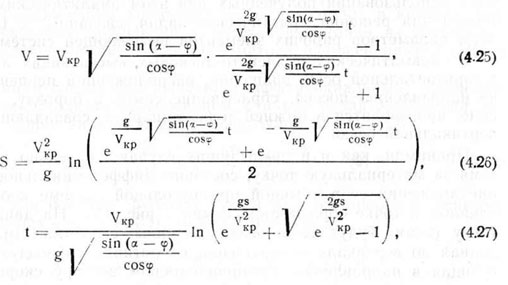
где а — угол наклона семяпровода (угол наклона прямой к оси х); Ф — угол трения семян.
Анализ зависимостей (4.25), (4.26) и (4.27) показывает, что при прочих постоянных условиях параметры движения семян по наклонному семяпроводу полностью и однозначно определяются физико-механическими свойствами семян и, в частности, скоростью витания и коэффициентом (углом) трения.
Следует отметить, что уравнения (4.18) —(4.24) могут быть использованы и для решения обратной задачи, т. е. для отыскания наиболее рационального вида скатных поверхностей (уравнения кривой), обеспечиваюших наперед заданные параметры движения семян, скажем, например, постоянство скорости падения их в борозду и т. д.
Выбрасывание семян высевающим аппаратом непосредственно в борозду без каких-либо на-правляющих и семяпроводящих устройств упрощает конструкцию рабочих органов высевающей системы и в некоторой степени снижает отрицательное влияние изменчивости физико-механических свойств семян на равномерность их распределения. В связи с этим данный вид транспортирования (движения)семян представляет интерес не только с точки зрения установления возможности его математического описания, но и в отношении дальнейшего использования полученных при этом аналитических зависимостей для решения практических задач, связанных с определением параметров рабочих элементов высевающей системы.
В пневматических и ячеисто-дисковых высевающих аппаратах с горизонтальной осью вращения, расположенной перпендикулярно направлению посева, сбрасывание семян в борозду, как правило, производится в нижней точке аппарата, совпадающей с его вертикальной осью.
Принимая, как и в предыдущих случаях, отдельно падающее семя за материальную точку, составим дифференциальное уравнение движения ее в обычной прямоугольной системе координат с началом в точке сбрасывания семян (рис. 4.7). На движущуюся точку (семя) будут действовать две силы: сила тяжести, направленная по вертикали вниз, и сила сопротивления воздуха, действующая в направлении, противоположном вектору скорости.
Рис. 4.7. К определению параметров движения семян при выбрасывании их высевающим аппаратом непосредственно в раскрытую сошником борозду.
Дифференциальные уравнения движения точки (семени) для данного случая (рис. 4.7) при R = kV2 имеет вид
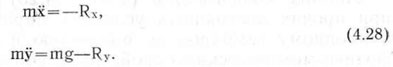
После подстановки значений Rx и Rz получим
Но, учитывая, что
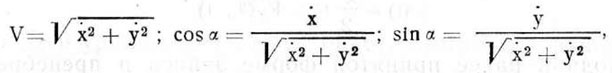
уравнения (4.29) можно записать так
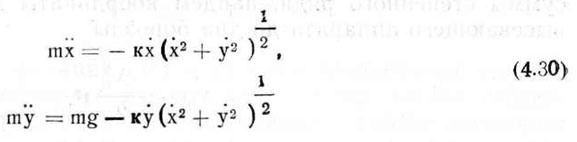
или сократив на массу и введя обозначения c = k/m, получим
Уравнения (4.31) в таком виде до конца не интегрируются, поэтому они решаются либо методами приближенного интегрирования (графически или численно) [102, 176], либо путем составления приближенных уравнений движения точки, в которые вводятся некоторые допущения и подстановки (один из возможных вариантов применения последнего метода изложен нами в работе [426]).
Б данном случае для решения дифференциальных уравнений (4.31) воспользуемся разложением функции в ряд Маклорена, который в общем виде выражается формулой
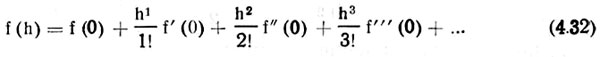
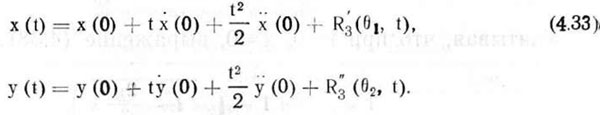
Используя начальные условия t = 0, находим
Подставив эти значения в уравнения (4.33), получим
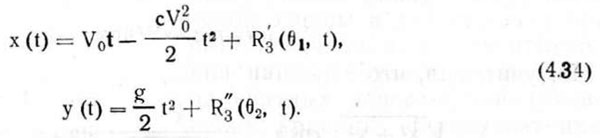
Переходя к ранее принятой форме записи и пренебрегая погрешностью, допущенной разложением искомых функций в виде суммы степенного ряда, найдем координаты движения семени от высевающего аппарата до дна борозды
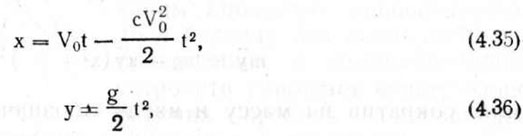
или, подставляя значение С и введя скорость витания, будем иметь
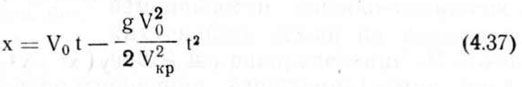
Для определения траектории движения семени выразим вначале из уравнения (4.37) t как функцию х.
Решая это уравнение, получим
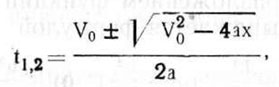
или, подставляя значение а, имеем
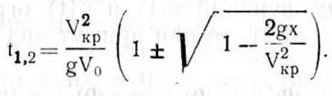(4.38)
Учитывая, что при t = 0, x = 0, выражение (4.38) примет вид
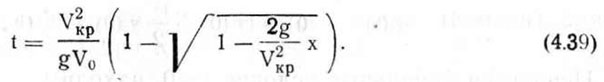
Из выражения (4.36) находим t в функции у
Далее, подставляя значение t из (4.39) в выражение (4.36), определим уравнение траектории движения семени
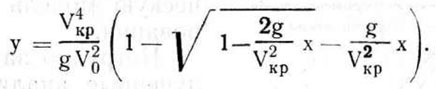(4.41)
Используя уравнения (4.37) и (4.40), найдем х в функции от у:
При определении функций x(t) и y(t) мы пренебрегли погрешностью, вызванной выбором ограниченного числа членов степенного ряда (ряда Маклорена), что, естественно, внесло некоторые ошибки в полученные зависимости. Для оценки величины этих ошибок дифференциальные уравнения (4.31) были решены также численным методом на электронно-вычислительной машине ЕС-1030. Сравнение результатов расчета на ЭВМ и по приведенной выше зависимости х(у) показывает (табл. 4.1), что в диапазоне начальных скоростей движения семян (Vo) от 0,1 до 0,2 м/с при высоте падения (у) и скорости витания семян (VI(p) соответственно от 0,05 до 0,2 м и от 2 до 6 м/с погрешность практически не превышает 5% и с увеличением Vo и VKP имеет четкую тенденцию к уменьшению.
В целях проверки полученных зависимостей были поставлены специальные лабораторные опыты с высевом семян томатов на неподвижный липкий экран. Траектории движения семян (рис. 4.8), построенные по данным опытов и результатам расчетов, имеют незначительные расхождения, что также свидетельствует о достаточной точности аналитических зависимостей, найденных путем приближенного решения дифференциальных уравнений (4.31).
Таким образом, рассматривая движение семян в процессе высева условно детерминированным и используя механико-математические методы анализа, мы установили аналитические зависимости между входными и выходными параметрами внутренней структуры высевающей системы, т. е. составили математическую модель ее функционирования.
Нетрудно заметить, что полученные аналитические зависимости для определения параметров движения семян в процессе высева являются функциями случайных аргументов. В частности, промежуток времени tn между выбрасыванием семян высевающим аппаратом является функцией случайных аргументов — времени одного оборота опорно-приводного колеса и коэффициента скольжения; время падения и разброс семян в борозде — функцией скорости витания, начальной скорости движения семян и внешнего трения. Это значительно, как будет показано ниже, упрощает построение математической модели высевающей системы 1 сеялки точного высева.
Выше мы касались только внутренней структуры высевающей системы. Теперь рассмотрим систему в целом и попытаемся дать ее математическое описание.
Таблица 4.1. Относительная погрешность определения функции х(у) i приближенным методом.
Рис. 4.8. Траектории движения семян от высевающего аппарата до дна борозды, построенные по данным опытов и теоретических расчетов (R=kV2).
Пусть посевной агрегат перемещается со скоростью V и семена высевающим аппаратом по одному через некоторые промежутки времени tOl по семяпроводу или непосредственно сбрасываются в раскрытую сошником борозду. Тогда величина отрезков пути, пройденных сеялкой за промежуток времени между выбрасываниями семян высевающим аппаратом {рис. 4.9), соответственно равна
При этом семена в борозде расположатся на некотором случайном расстоянии х1, х2, х3, ..., хn-1 и хn от соответствующих точек выброса 1, 2, 3, ..., n—1, n.
Согласно этому, значения интервалов между семенами определятся из равенств
Рис. 4.9. К определению числовых характеристик распределения интервалов между семенами при односемянном посеве (при условии отсутствия инверсий).
Подставив в эти равенства значения а, получим
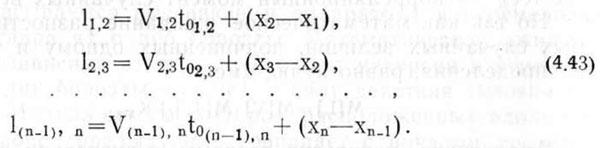
Из выражения (4.43) видно, что интервалы между семенами в рядке являются функциями случайных величин v, to и X, т. е. скорости движения агрегата, промежутка времени между выбрасыванием семян высевающим аппаратом и величины отклонения семян от точек сбрасывания.
Среднее арифметическое и дисперсия интервалов между семенами, согласно выражению (4.43), определятся по формулам
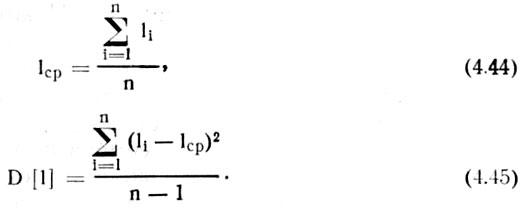
При неограниченном увеличении числа опытов (числа замеряемых интервалов), т. е. при n → ∞ выражения (4.44) и (4.45), согласно теореме Чебышева [111], могут служить оценками для математического ожидания и дисперсии интервалов между семенами в рядке.
Тогда, используя общепринятую форму записи функций случайных величин, равенство (4.43) примет вид
где L — функция случайных величин (интервал между семенами); V, Тn, X — случайные величины, соответственно скорость движения агрегата, промежуток времени между выбрасыванием семян высевающим аппаратом, отклонение семян от точек сбрасывания.
Для определения математического ожидания и дисперсии интервалов воспользуемся теоремами о числовых характеристиках функций случайных величин [111].
В общем случае, согласно теореме сложения математических ожидании, имеем
Используя теорему умножения математических ожиданий, получим
где KVt° - корреляционный момент случайных величин V и То.
Но так как математическое ожидание разности двух независимых случайных величин, подчиненных одному и тому же закону распределения, равно нулю, имеем:
Аналогично, используя теоремы о дисперсии функции случайных величин, находим
где mv, т — математические ожидания соответственно скорости движения агрегата и промежутка времени между выбрасыванием семян высевающим аппаратом.
Вопрос о характере изменения скорости движения посевного агрегата является дискуссионным. Некоторые авторы в подобного рода исследованиях считают (принимают) ее постоянной величиной, другие — относят к числу случайных. Применительно к нашему случаю она, безусловно, изменяется в процессе движения агрегата и оказывает соответствующее влияние на процесс образования интервалов между семенами в рядке. Но учитывая, что плотность посева семян большинства овощных культур на длине рядка в один метр находится в пределах от 20 до 200 шт., а колебания скорости на пути такой протяженности (один метр) весьма незначительны, то в первом приближении величину скорости движения посевного агрегата, входящую в выражения (4.48) и (4.49), можно принять постоянной.
Тогда при V = const выражения (4.48) и (4.49) примут вид
Случайная величина Х со скоростью движения агрегата связана очевидным соотношением (рис. 4.9) x = Vt, где t — время движения семян от высевающего аппарата до дна борозды {случайная величина).
С учетом этого соотношения дисперсия случайной величины X равна
Подставляя (4.52) в выражение (4.51), получим
Выражения (4.50) — (4.53) для математического ожидания и дисперсии интервалов определены без учета влияния инверсий (несоответствий порядка чередования семян в рядке порядку, в котором они выбрасываются высевающим аппаратом) и перемещений семян после удара их о дно борозды. Математическое ожидание интервалов, независимо от того, происходят инверсии и перемещения семян по дну борозды или нет, в силу действия условия теоремы Шаля («Модуль суммы векторов, расположенных вдоль прямой так, что конец предыдущего совпадает с началом последующего, равен расстоянию между началом первого вектора и концом последнего»), остается постоянным.
Для учета влияния перемещения семян по дну борозды на величину дисперсии интервалов введен коэффициент (i, численно равный отношению дисперсий, полученных в опытах при высеве семян в борозду и на липкую ленту
где 
— дисперсия интервалов при высеве в борозду; 
— дисперсия интервалов при высеве на липкую ленту в тех же условиях.
Проведенные нами эксперименты [481] показали, что коэффициент ц, при посеве на скоростях до 3,34 м/с по обычно подготовленной почве (объемная масса 1100—1400 кг/м3) с высотой расположения высевающих аппаратов до 0,2 м находится в пределах 1,1—1,6. При этом меньшее значение коэффициента относится к борозде клиновидной формы, большее — к плоской.
Инверсии в распределении семян возможны тогда и только тогда, когда время падения (движения) предыдущего семени будет больше, чем сумма времени падения последующего и промежутка времени между выбрасыванием семян, т. е.
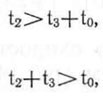
где t2, t3 — соответственно время падения предыдущего и последующего семени.
Экспериментально-теоретическими исследованиями [481] установлено, что при высоте расположения высевающего аппарата овощной сеялки точного высева до 0,2 м и шаге посева (расстояние между семенами в рядке) от 0,05 м и выше инверсии в распределении семян на скоростях посева до 3,34 м/с практически не наблюдаются. Поэтому в рассматриваемой высевающей системе их можно не учитывать.
Согласно вышеизложенным » соображениям и полученным ранее данным экспериментов, выражения (4.51) и (4.53) примут вид
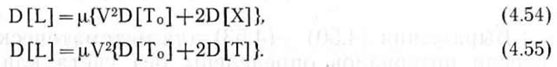
Таким образом, мы установили функциональную связь между параметрами внутренней структуры высевающей системы и ее выходным показателем, характеризующим равномерность распределения интервалов между семенами в рядке, выраженную через их математические ожидания и дисперсии.
Используя полученные ранее аналитические зависимости 
между параметрами внутренней структуры высевающей системы (рис. 4.3а), найдем значения математического ожидания и дисперсий, выходящих в выражения (4.50), (4.54) и (4.55).
В общем виде математическое ожидание и дисперсия функции одного случайного аргумента определяется из выражений:
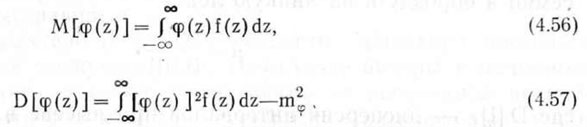
где f(z) — плотность распределения случайной величины Z; тФ = M[cp(z)] — математическое ожидание функции tp(z).
Аналогично находят математическое ожидание и дисперсию функции двух случайных аргументов
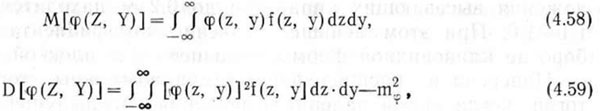
где mф = М[ф(z, у)] — математическое ожидание функции <p(z, у); f(z, у) — совместная плотность распределения системы случайных величин (Z, Y).
Промежуток времени to между выбрасыванием семян высевающим аппаратом, как это видно из выражения (4.12), не зависит от способа транспортирования семян до дна борозды и является линейной функцией случайного аргумента tK — времени одного оборота опорно-приводного колеса сеялки. Поэтому для рассматриваемой высевающей системы математическое ожидание и дисперсию промежутка времени to можно вычислить по формулам
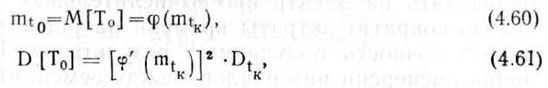
где mtk и Dtк — математическое ожидание и дисперсия времени одного оборота опорно-приводного колеса; ф'(mtk) — производная функции промежутка времени между выбрасыванием семян в точке, соответствующей математическому ожиданию аргумента tк, т. е. математическому ожиданию одного оборота опорно-приводного колеса.
Тогда, используя зависимость (4.12) и формулы (4.60) и (4.61), найдем окончательные выражения для вычисления математического ожидания и дисперсии промежутка времени между выбрасыванием семян высевающим аппаратом рассматриваемой системы
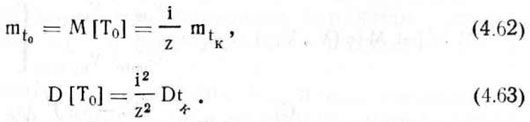
Таким образом, математическое ожидание и дисперсия промежутка времени между выбрасыванием семян высевающим аппаратом полностью определяются числовыми характеристиками оборотов опорно-приводного колеса сеялки, его кинематической связью с высевающим аппаратом и числом ячеек или присасывающих отверстий высевного устройства.
Время движения семян от высевающего аппарата до дна борозды (t) и отклонение их от точек выбрасывания (х), как было показано выше, являются функциями случайных аргументов, вид и число переменных которых зависит от способа транспортирования семян и конструктивных особенностей семяпроводов. В частности, при свободном падении семян в вертикально установленном семяпроводе (кожухе) время движения и путь, пройденный семенем, являются функциями одного случайного аргумента — скорости витания семян (4.16), (4.17); при движении по наклонному семяпроводу — скорости витания и коэффициента внешнего трения семян (4.26), (4.27); при подаче семян непосредственно в борозду — парусности и начальной скорости движения семян (4.39), (4.42).
Следовательно, подставляя соответствующее значение функций в выражения (4.56) и (4.57) или в (4.58) и (4.59), а также учитывая, что скорость витания (VKp), коэффициент внешнего трения (f) и начальная скорость движения семян (Vo) между собой независимы (некоррелированы) и подчиняются нормальному закону распределения, найдем математическое ожидание и дисперсии времени движения семян от высевающего аппарата до дна борозды и отклонения их от начальных точек сбрасывания (разброс траекторий падения семян) для каждого вида транспортирования семян.
Указанные числовые характеристики функций целесообразно определять на электронно-вычислительных машинах, что значительно сократит затраты времени на расчеты и обеспечит необходимую точность получаемых результатов. При этом для вычисления дисперсии интервалов между семенами в рядке высевающей системы с транспортированием семян по семяпроводам более удобно пользоваться зависимостью (4.55), при подаче семян непосредственно в борозду — зависимостью (4.54). Согласно этому, под знаком интегралов выражений (4.56) —(4.59) берутся соответственно функции t(h) и x(h), т. е. t(y) и х(у).
Для высевающей системы сеялок точного высева с подачей семян непосредственно в борозду математическое ожидание и дисперсия случайной величины X — отклонение семян от точки выброса — вычисляются по формулам (4.58) и (4.59) при подстановке в них значения функции х = ф(Уо, VKp) согласно выражению (4.42)
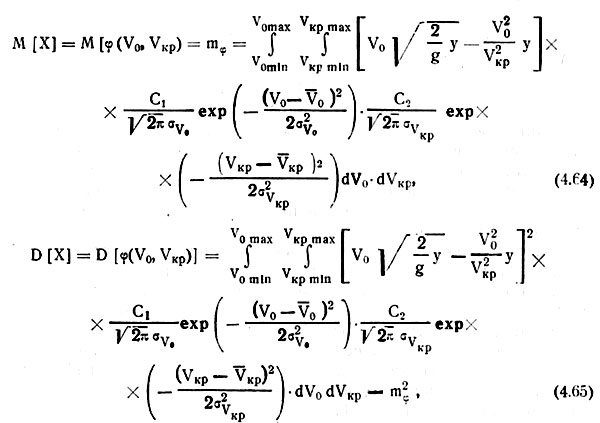
где 
- минимальные и максимальные значения соответственно начальной скорости движения и скорости витания семян; Vo и Vкp — среднее арифметическое начальной скорости движения и скорости витания семян; σ (Vo), σ (Vкр) — среднее квадратическое отклонение начальной скорости движения и скорости витания семян; mφ — математическое ожидание функции φ (Vo, Vкp);
Коэффициенты C1 и С2 учитывают изменение плотности распределения случайных величин (аргументов) Vo и Vkp, вызванное усечением нормального распределения, т. е. изменением пределов интегрирования. В строгом смысле, случайные аргументы рассматриваемой функции являются дискретными. Но так как семена большинства овощных культур очень мелкие и при статистическом методе определения показателей физико-механических свойств в каждом классе их содержится от 300 до 2000 шт., то с некоторым приближением можно считать, что аргументы являются непрерывными случайными величинами. Кроме того, поскольку вычисление значений математических ожиданий и дисперсий функций осуществляется численным методом на электронно-вычислительных машинах, то принятое допущение о непрерывном характере случайных аргументов не приводит к существенным погрешностям в расчетах.
Следует также отметить, что значения Vкр и σкр, входящие в выражения (4.64) и (4.65), сами по себе являются параметрами усеченного распределения. Но так как степень усечения, т. е. вероятность того, что случайная величина VKP окажется вне интервала (Vкp min, Vкp max), очень мала (0,0097), то исходные значения Vкр и σVкр можно принять за параметры нормального неусеченного кр распределения.
Подставив в уравнения (4.50) и (4.54) значения входящих в них величин, согласно выражениям (4.62) и (4.65), получим
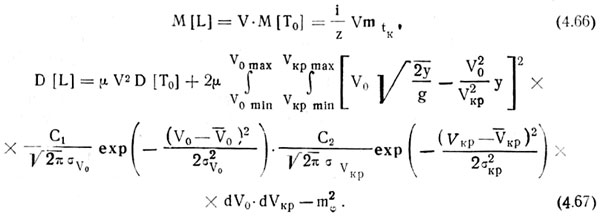
Анализ зависимостей (4.66) и (4.67) показывает, что они не только характеризуют внутреннюю структуру рассматриваемой высевающей системы, но и устанавливают функциональную связь ее основных параметров с выходными показателями, определяющими равномерность распределения семян, т. е. математическим ожиданием и дисперсией интервалов между семенами в рядке. При наличии такой связи дальнейшее построение математической модели функционирования высевающей системы сеялок точного высева значительно упрощается и в общем виде сводится к установлению экспериментальным путем (методом идентификации) вида оператора Ai (см. рис. 4.3а), связывающего внешние входные переменные Qi(L) с одним основным внутренним воздействием TK(Q).
Если же в качестве входного воздействия высевающей системы принять показатель T (Q) — изменчивость скорости вращения опорно-приводного колеса сеялки — или время между выбрасыванием семян высевающим аппаратом, характеризующие совокупное действие всех внешних возмущений (качество подготовки почвы) [151], то для построения математической модели (оператора) рассматриваемой системы оказывается вполне достаточным экспериментально определить числовые характеристики времени одного оборота опорно-приводного колеса сеялки или времени между выбрасыванием семян, скорости витания высеваемых семян и поправочный коэффициент, учитывающий влияние профиля борозды на величину дисперсии интервалов между семенами.
(Таким образом, применение принципов механики и теории случайных функций, т. е. комбинированного механико-статистического- метода, значительно упрощает построение математической модели функционирования сеялок точного высева и дает возможность до минимума свести объем экспериментальных и вычислительных работ. Кроме того, этот метод в отличие от метода идентификации позволяет характеризовать не только поведение системы в целом, но и устанавливать влияние ее конструктивного оформления и свойств высеваемого материала на конечные результаты посева, т. е. позволяет на стадии проектирования определять оптимальные параметры рабочих органов высевающей системы в зависимости от заданных выходных показателей, характеризующих равномерность распределения семян на засеваемом поле.
Математическая модель высевающей системы,
разработанная нами на основе механико-статистического метода, использовалась
при исследовании распределения семян овощной сеялки точного высева СОПГ-4,8.
Для этого экспериментальным путем были определены числовые характеристики и
законы распределения (рис. 4.10) скорости витания высеваемых семян, промежутка
времени между выбрасыванием семян высевающим аппаратом и начальной скорости
движения семян, а также поправочный коэффициент X. По этим исходным данным
(табл. 4.2, 4.3, 4.4) и зависимостям (4.66) и (4.67) на ЭВМ ЕС-1030 определялись
теоретические значения математического ожидания и дисперсии интервалов; между семенами в рядке, которые сравнивались с результатами полевых опытов (табл. 4.5 и 4.6).
Рис. 4.10. Кривые плотности распределения случайных величин.
Из табл. 4.6 видно, что числовые характеристики распределения интервалов между семенами в рядке (математическое ожидание и дисперсия), рассчитанные по найденным аналитическим зависимостям и по информации, полученной в опыте, достаточно хорошо согласуются между собой. Некоторое несовпадение значений этих показателей, вероятно, объясняется естественным рассеиванием семян, обусловленным асимметрией их форм, а также колебаниями передаточного отношения привода высевающего аппарата, которые не учитывались при теоретическом , анализе высевающих систем.
Замечено, что применение цепных передач в приводе высевающих аппаратов, особенно с большим передаточным отношением, отрицательно влияет на равномерность промежутков времени между выбрасыванием семян и их начальную скорость движения, а следовательно, и на равномерность распределения интервалов между семенами.
Анализ структуры дисперсии интервалов (см. табл. 4.6) показывает, что из общей её величины основная часть (95—99%) приходится на составляющую, определяемую дисперсией промежутка времени между выбрасыванием семян, и значительно меньшая — на составляющую, зависящую от рассеивания траектории падения семян. Однако с увеличением высоты падения семян последняя составляющая резко возрастает и при h = 0,5 м достигает 18% от общей дисперсии.
Важным мероприятием в повышении равномерности распределения семян при односемянном и гнездовом посевах является качественная предпосевная обработка почвы. Установлено, что фрезерная подготовка почвы и движение опорно-приводных ко¬лес сеялки по колее трактора значительно снижают колебания скорости вращения последних, а следовательно, и промежутков времени между выбрасыванием семян высевающим аппаратом.
Точный гнездовой посев семян овощных культур, согласно агротехническим требованиям, характеризуется интервалами между центрами высеянных гнезд, количеством и компактностью рас-положения семян в гнезде.
В соответствии с этим анализ и синтез высевающей системы гнездовых сеялок точного высева по основным показателям — математическому ожиданию и дисперсии интервалов между гнездами — может быть выполнен по описанной выше математической модели функционирования односемянных (пунктирных) сеялок.
Таблица 4.2. Вариационный ряд и числовые характеристики распределения витания скорости семян томатов (сорт VF-134).
Таблица 4.3. Вариационные ряды и числовые характеристики распределения промежутка времени между выбрасыванием семян высевающим аппаратом овощной сеялки точного высева СОПГ-4,8 (томаты, сорт VF-134).
Таблица 4.4. Вариационные ряды и числовые характеристики распределения начальной скорости движения семян от высевающего аппарата сеялки СОПГ-4,8 до дна раскрытой сошником борозды (томаты, сорт\Т-134).
Таблица 4.5. Вариационные ряды и числовые характеристики распределения интервалов между семенами в рядке при гнездовом посеве томатов сеялкой СОПГ-4,8 (данные полевых опытов; сорт УГ-134, заданный шаг посева — 0,21 м).
Таблица 4.6. Равномерность распределения интервалов между семенами в рядке при гнездовом посеве томатов сеялкой СОПГ-4,8* (сорт VF-134, заданный шаг посева —0,21 м).
Рис. 4.11. К определению максимальной длины гнезда при гнездовом посеве.
Количество семян, высеваемых в гнездо, в общем случае определяется конструктивными особенностями и режимными параметрами дозирующих и гнездообразующих устройств высевающей системы. В овощных гнездовых сеялках с механическими высевающими аппаратами ячеисто-дискового и ячеисто-ленточного типа этот показатель в основном зависит от формы, объема и геометрических параметров ячеек, а также от скорости вращения высевных дисков и лент, которая, при прочих равных условиях, является главным фактором заполняемости ячеек, а следовательно, и стабильного дозирования заданного количества семян, высеваемых в одно гнездо.
Теория процесса заполнения ячеек, основанная еще акад. В. П. Горячкиным, в настоящее время получила широкое развитие и достаточно полно освещена в трудах акад. П. М. Василенко, Г. М. Рудакова, А. А. Будагова, В. С. Васина и других советских и зарубежных ученых [63, 65, 89, 109, 411]. Поэтому в данной работе мы остановимся лишь на выборе (расчете) геометрических параметров ячеек высевного барабана пневматических сеялок гнездового посева.
Рис. 4.12. К определению длины гнезда при экранировании вакуума наклонной и вертикальной стенкой.
Разброс семян в гнезде (компактность гнезд) зависит от ряда факторов, основными из которых являются физико-механические свойства самих семян (форма, парусность, упругость), начальная скорость выбрасывания их высевающим аппаратом, твердость почвы и профиль борозды.
В общем случае при заданной высоте расположения высевающего аппарата (точки сбрасывания семян) от дна борозды максимально возможная длина гнезда, вызванная изменчивостью физико-механических свойств семян, определится из равенства (4.42) при подстановке в него максимальных и минимальных значений скорости витания семян и их начальных скоростей движения (рис. 4.11):
где δ — длина гнезда; μ — коэффициент, учитывающий перекатывание семян по дну борозды, определяемый экспериментально.
На длину гнезда существенное влияние оказывает неодновременность сбрасывания семян высевающим аппаратом, обусловленная в механических ячеисто-дисковых и ячеисто-ленточных аппаратах неравномерностью разгрузки ячеек, в пневматических — неодновременным экранированием вакуума, т. е. перекрытием присасывающих отверстий.
В пневматических сеялках с высевающими аппаратами дискового типа для высева семян гнездами используются диски с групповым размещением присасывающих отверстий (рис. 4.12). Экранирование вакуума в таких аппаратах осуществляется, как правило, перекрытием присасывающих отверстий задней стенкой камеры разрежения. Компактность размещения семян и длина гнезда в данном случае во многом зависят от взаимного расположения присасывающих отверстий и задней экранирующей стенки камеры разрежения. Ниже приводятся формулы для расчета длины гнезда при треугольном размещении присасывающих отверстий с наклонной и вертикальной задней стенками. Такое расположение отверстий используется во многих современных конструкциях овощных пневматических сеялок для гнездового посева.
Для наклонной экранирующей стенки (плоскость 1—1, см. рис. 4.12) длина гнезда, обусловленная несоответствием моментов перекрытия присасывающих отверстий, может быть рассчитана по формуле
где V — скорость движения посевного агрегата, м/с; ω — угловая скорость высевного диска (присасывающих отверстий), с-1; φ — угол поворота диска в радианах; g — ускорение силы тяжести, м/с2; r1, r2, r3 — радиусы окружностей, на которых расположены присасывающие отверстия, м.
Выражение, стоящее в круглых скобках правой части формулы (4.69), учитывается в том случае, если представленная им разность положительна, т. е. больше нуля. Физически это соответствует тому, что семя I после экранирования вакуума быстрее достигнет точки С, нежели семя 3 точки Д, т. е. семя 3 после экранирования будет перемещаться за семенем I и при падении в борозду увеличит длину гнезда. Если же дробное выражение в круглых скобках правой части формулы (4.69) окажется меньше нуля, то это означает, что семя 3 раньше семени 1 подошло к точке Д, т. е. раньше сэкранировалось, чем семя I успело подойти к точке С. В результате этого семя 3 в борозде займет положение между вторым и первым семенами, не увеличивая длину гнезда. Поэтому в данном случае выражение в круглых скобках не учитывается.
Аналогичная картина наблюдается и при наклонной экранирующей стенке. Здесь в отличие от предыдущего берется точка В и не учитывается последний член выражения (4.70), если разность, стоящая в круглых скобках, отрицательна. Физически это означает, что семя I в борозде займет , положение между вторым и третьим семенами, т. е. общая длина гнезда будет определяться положением второго и третьего семян. Кроме того, первые два члена правой части выражения (4.70) берутся по модулю и к их разности (не обращая внимания на знак) прибавляются остальные с учетом сказанного выше.
В некоторых конструкциях .пневматических овощных сеялок при гнездовом высеве экранирование вакуума в присасывающих отверстиях, расположенных по углам правильного треугольника (см. рис. 4.12), осуществляется одновременно. Такой способ экранирования, в частности, использован на отечественной овощной сеялке точного высева СУПО-6. Это достигается специальной конструкцией высевного диска и размещением присасывающих отверстий на тонком накладном дне цилиндрической ячейки. Поэтому при выходе ячейки из зоны разрежения вакуум на всех трех присасывающих отверстиях снимается одновременно.
В указанной сеялке экранирование вакуума в ячейках производится в вертикальной плоскости, проходящей через ось высевающего аппарата, т. е. при а = 0 (см. рис. 4.12). Для этого случая вы-ражение (4.69) с учетом оговоренных выше замечаний примет вид
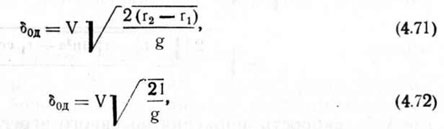
где l = r2 - r1 — расстояние между первыми двумя отверстиями.
Расчеты по формуле (4.72) показывают, что несмотря, казалось бы, на незначительное расстояние между первыми двумя отверстиями (0,0035 м), длина гнезда при посеве семян томатов сеялкой СУПО-6 на скоростях в 1,39; 1,94 и 2,5 м/с (5, 7 и 9 км/ч), без учета действия других факторов, составляет соответственно 0,037; 0,052 и 0,067 м, что при наиболее распространенном шаге посева 0,15-0,20 м значительно превышает расстояния, допустимые агротехническими требованиями на гнездовой посев овощных культур. Приведенные расчеты полностью соответствуют данным Государственных испытаний сеялки СУПО-6 и свидетельствуют о том, что указанные варианты размещения присасывающих отверстий и способы экранирования вакуума в пневматических дисковых аппаратах для гнездового посева семян овощных культур являются неприемлемыми и требуют уточнения.
Рис. 4.13. К определению длины гнезда при трехрядном расположении присасывающих отверстий.
На рис. 4.13 приведена схема размещения присасывающих отверстий для дискового высевающего аппарата, согласно которой длина гнезда может быть сведена до минимума, вполне удовлетворяющего агротехническим требованиям.
Расчеты размещения отверстий в соответствии с этой схемой могут быть выполнены исходя из условий, выраженных следующими равенствами (приводятся без выводов)
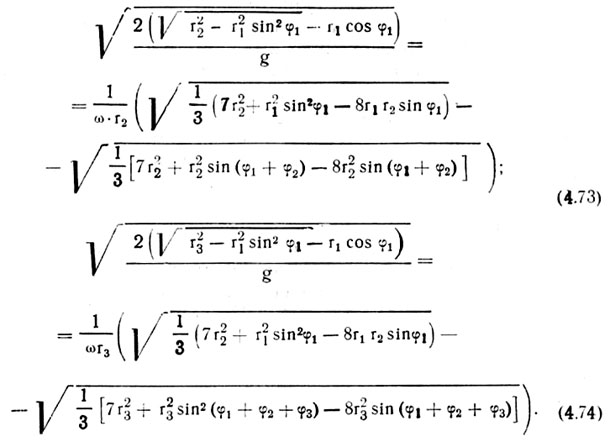
Выражения (4.73) и (4.74) получены из условий равенства времени движения семени от первого присасывающего отверстия (после его экранирования) до точек А и В (см. рис. 4.13) и времени движения второго и третьего присасывающих отверстий соответственно до тех же точек А и В.
При известных геометрических и режимных параметрах высевного диска, задавшись положением первого присасывающего отверстия (ф1 и ri ) и радиусами г2 и г3, по выражениям (4.73)* и (4.74)*, определяем соответственно углы ф2 и фз, т. е. положения второго и третьего присасывающего отверстия.
При экранировании вакуума в плоскости, совпадающей с вертикальной осью высевного диска, т. е. при ф=0, выражения (4.73) и (4.74) значительно упрощаются и принимают вид
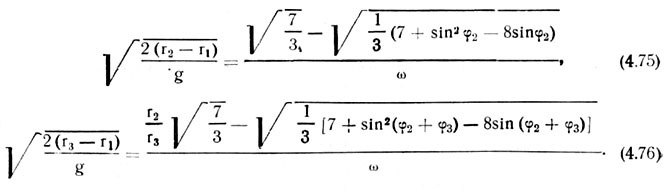
В пневматических высевающих аппаратах барабанного типа присасывающие отверстия для высева семян группами (гнездами) обычно располагаются в один ряд по образующей цилиндрической поверхности барабана или в ячейках, что обеспечивает практически одновременное экранирование вакуума, а следовательно, более компактное размещение семян в гнезде.
Таким образом, приведенные формулы для определения длины гнезда и полученные ранее аналитические зависимости (математическая модель) образования интервалов между семенами (гнездами) могут служить основой для анализа и синтеза высевающей систем,ы гнездовых сеялок точного высева.
Основными рабочими элементами посевных машин, определяющими равномерность глубины заделки семян, являются бороздо- образующие, заделывающие и прикатывающие устройства, объединенные в так называемые сошниковые системы (посевные секции).
Изучение условий работы сошниковых систем сеялок точного высева показало, что на равномерность глубины хода сошника (равномерность глубины заделки семян), наряду с неровностями поверхности поля, влияют колебания твердости почвы и рамы сеялки [77, 152, 163, 231, 300, 438]. Поэтому в последнее время при исследовании динамики сошниковых систем используются многомерные динамические модели, отражающие влияние указанных факторов (см. рис. 4.36). Однако ни в одной из предложенных моделей, описанных в указанных работах, не учитываются сдвиги (запаздывания) в действии возмущающих факторов и так называемые «последействия», обусловленные пространственной протяженностью посевных секций и последовательным расположением на них рабочих органов.
Сущность последействия заключается в том, что всякое отклонение сошника фиксируется в профиле образуемой им поверхности, движение катка по которой приводит к зависимости текущего положения сошника от его предыдущего положения. У двухопорных сошниковых систем такая взаимосвязь существует и между положениями переднего катка и сошника.
Влияние последействия на динамику почвообрабатывающих машин приводится в работах В. А. Ксендзова [265, 266]. Однако в них рассматривается только кинематическая сторона процесса, связанная с копированием поверхностей, образованных впереди идущими рабочими органами. В то же время при работе реальных машин последействие проявляется и в изменении механических характеристик почвы (плотности, твердости, коэффициента объемного смятия и др.) в каждой данной точке поля, что влечет за собой изменение сил сопротивления почвы и ее деформаций. В связи с этим последействие должно учитываться при разработке моделей.
Для построения математической модели функционирования сошниковой системы сеялки точного высева, согласно структурной схеме, приведенной на рис. 4.36, воспользуемся аналитическими методами, содержание и порядок применения которых подробно изложены в работах акад. П. М. Василенко [103, 104, 105, 106, 107, 108]. Одним из ответственных моментов использования этих методов является выбор эквивалентной схемы, отражающей степень идентичности модели реальному объекту. Построение эквивалентной схемы начинается с идеализации рассматриваемого технического объекта, в данном случае сошниковой системы.
Предположим, что:
- движение агрегата прямолинейно, равномерно и рассматривается
в продольно-вертикальной плоскости;
- все элементы агрегата являются недеформируемыми телами;
- характеристики упругих элементов линейны;
- на рабочие органы агрегата действуют сосредоточенные силы сопротивления почвы, являющиеся функциями координат и скоростей характерных точек этих органов;
- диссипативные силы прямо пропорциональны скоростям
движения рабочих органов;
- почва рассматривается как сплошная среда;
- все стохастические процессы описываются стационарными случайными функциями.
Рис. 4.14. Расчетная схема сошниковой системы сеялки точного высева.
К этому следует добавить, что цилиндрические опорные катки сошниковой секции имеют одинаковые геометрические размеры и массы.
Принятые допущения позволяют представить эквивалентную модель двухопорной сошниковой секции в виде системы твердых тел: поводка, сошника с высевающим аппаратом, рамки тележки, переднего и заднего опорных катков с массами, соответственно, mn, m,., nip, т„ и моментами инерции: Jn, Jt, Jp, Jк.
Движение сошниковой секции будем рассматривать в неподвижной системе декартовых координат XOY, связанной с почвой (рис. 4.14). Ось OY направлена вертикально вниз, а ось ОХ — горизонтально по направлению движения и расположена на высоте Но от средней линии неровностей поверхности поля. С брусом сеялки связана подвижная система отсчета Хь Oi,Yi. Ось OiYi направлена вертикально вниз, а ось OXi — горизонтально и противоположно оси ОХ. В начальный момент времени точки Oi и О совпадают. Система координат X2O2Y2 связана с рамкой тележки.
На сошниковую систему наложены связи в виде рамы сеялки, поверхности поля и позиционные связи вида
Если рассматривать силы трения в связях (шарниры, почва) как активные силы, которые можно привести к диссипативным моментам М1 и М2, то связи, наложенные на сошниковую систему, будут идеальными.
Уравнения движения рамы сеялки, согласно принятым допущениям, имеют вид
где xо1— горизонтальная составляющая скорости движения рамы сеялки, хо1 = const.
Если пренебречь проскальзыванием опорных катков секции, то на нее будут наложены кинематические связи вида [292] (рис. 4.15):
где VAj — вектор скорости оси катка; ф — угловая скорость катка; г, — радиус-вектор мгновенного центра вращения катка. Условие (4.79) в случае плоскопараллельного качения приводит к уравнениям
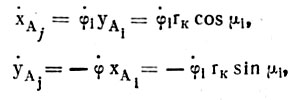
где rK — радиус катка; μ1 — угол отклонения радиус-вектора r1 от вертикали, обусловленной неровностями поверхности поля. Полагая угол μ1 малым, можно считать, что 
, тогда
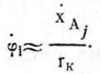
Отсюда следует, что связи, наложенные на катки, являются голономными. Следовательно, выбранная модель сошниковой системы имеет две степени свободы и ее положение однозначно определяется обобщенными координатами ср и у (см. рис. 4.14).
На сошниковую систему действуют следующие силы: давление нажимной пружины Fo, вес поводка Рп, рамки тележки Рр, сошника с высевающим аппаратом Рг, катков Рк и сопротивление почвы Fb F,., F2.
Рис. 4.15. Схема качения опорного катка сошниковой секции.
Экспериментальными исследованиями процесса взаимодействия сошниковой системы с почвой установлено, что система «сошник—почва» обладает большим демпфированием [381, 511]. Поэтому в расчетной схеме учтены силы трения рабочих органов о почву, которые для простоты приведены к диссипативцым моментам M1 и М2, пропорциональным соответствующим обобщенным скоростям
где ε1, ε2 — коэффициенты пропорциональности.
Существует несколько методов составления дифференциальных уравнений динамики систем с голономными связями — с помощью уравнения Даламбера-Лагранжа, общих теорем динамики, уравнений Лагранжа второго рода или канонических уравнений Гамильтона.
Наиболее удобным и эффективным из них является метод, основанный на использовании уравнений Лагранжа второго рода [104, 108]. Наряду с вычислительными преимуществами, по сравнению с первыми двумя методами уравнения Лагранжа представляют собой алгоритм составления уравнений движения системы, благодаря чему вероятность логических ошибок резко снижается.
Поэтому для составления уравнений движения сошниковой системы были использованы уравнения Лагранжа второго рода.
где Т — кинетическая энергия системы; Qj — обобщенная сила; cjj — обобщенная координата (q1=α, q2 = γ).
Кинетическая энергия системы равна
где Те — кинетическая энергия переносного движения системы; Тm — группа слагаемых, представляющих линейную функцию обобщенных скоростей; Тr — кинетическая энергия относительного движения.
В общем случае составляющие Tе, Tm и Тr кинетической энергии системы материальных точек определяются выражениями
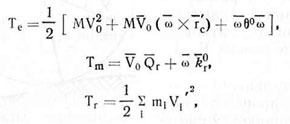
где М — масса сошниковой секции, Θ0 — ее тензор инерции в точке 01; Vo — скорость полюса подвижной системы XiOiYt, ω - ее угловая скорость; г. — радиус-вектор центра инерции сошниковой секции; Qr — главный вектор относительных количеств движения секции; Кг — главный момент относительных количеств движения секции относительно полюса О, — масса элемента сошниковой секции; Vi — скорость элемента секции относительно подвижной системы Xi OjYi. В силу допущения о поступательном движении рамы сеялки о) = 0, тогда
Главный вектор Qr относительных количеств движения системы определяется по формуле [292]
Запишем выражения для векторов Vo и Vi в проекциях на оси координат, соответственно, XOY и X,OiY,
где i, j и ii, j i — орты осей системы отсчета XOY и XLOiYi.
Подставляя зависимости (4.86), (4.87) и (4.88) в формулу (4.85) и выполнив необходимые преобразования, с учетом того, что i-ii= — 1, ]-ji = l, получим
Согласно теореме Кёнига, кинетическая энергия твердого тела, совершающего плоскопараллельное движение, равна
где J) — момент инерции твердого тела.
Поэтому для составляющей Тг кинетической энергии сошниковой системы можно записать
причем для поводка ω1 = α, а для тележки ω1 = γ .
Общее выражение кинетической энергии сошниковой системы имеет вид
Координаты центров масс элементов сошниковой системы в подвижной системе осей XiOiY, определяются по формулам
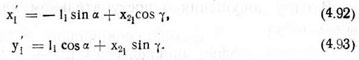
Для точек, находящихся на поводке, х21 = 0, а для точек тележки l1 = ln. Моменты инерции элементов сошниковой системы равны
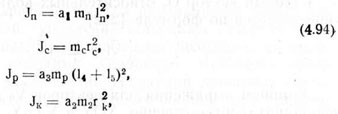
где α1, α2, α3 — коэффициенты, учитывающие распределение масс; ln = O1O2; l4 = О2А4; l5 = O2A5; rc — радиус инерции сошника с высевающим аппаратом; гк — радиус катка.
Продифференцировав координаты центров масс (4.92) и (4.93) по времени и подставив полученные выражения в формулу (4.91) найдем кинетическую энергию сошниковой системы
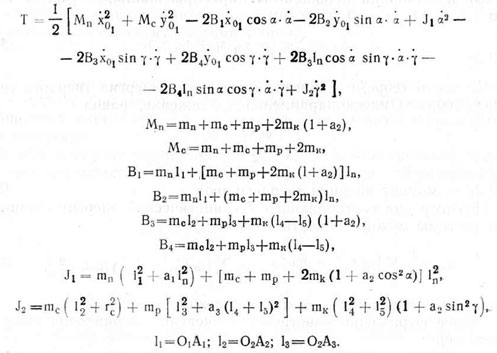
Для определения обобщенных сил составим сумму элементарных работ δ'ω сил R1, и моментов Mj, приложенных к системе, на виртуальных перемещениях δri и δqj точек приложения этих силовых факторов
Положения точек приложения сил в инерционной системе определяются радиус-векторами
где r0 — радиус-вектор полюса О1, заданная функция времени; r1 — радиус-вектор точки приложения силы в подвижной системе
отсчета XiOiYj.
Так как виртуальные перемещения δr1, находятся в фиксированный момент времени, то 
Запишем выражения для векторов R, и г, в проекциях, соответственно, на оси XOY и XiOjYi
где Rix, Riy — проекции сил, действующих на сошниковую систему. Подставив выражения (4.98) и (4.99) в формулу (4.97) и выполнив необходимые преобразования, получим
Из выражения (4.100) найдем обобщенные силы
— горизонтальная и вертикальная координаты точки А6 в системе отсчета Х2О2У2.
Подставив в уравнение (4.82) значения кинетической энергии (4.91) и обобщенных сил (4.101), (4.102), получим дифференциальные уравнения движения сошниковой системы
Таким образом, движение двухопорной сошниковой системы описывается системой двух нелинейных дифференциальных уравнений второго порядка. Для решения этой системы необходимо найти силы сопротивления почвы, действующие на сошник и опорные клетки.
Наибольшие трудности при изучении динамики сельскохозяйственных машин вызывает определение обобщенных сил и особенно той их части, которая связана с сопротивлением почвы. Это обусловлено отсутствием в настоящее время аналитических зависимостей, достаточно точно описывающих силовое взаимодействие рабочих органов с почвой.
В общем случае почва обладает одновременно упругими, пластическими и вязкими свойствами, которые в зависимости от конкретных условий проявляются по-разному, что в итоге определяет и различный характер протекания деформационных процессов. Неоднородность механического состава и строения почвы, колебания влажности приводят к тому, что процесс взаимодействия имеет статистический характер, в результате силы сопротивления представляют собой случайные функции времени (пути) и не могут быть выражены в виде детерминированных зависимостей.
При исследовании динамики сельскохозяйственных машин зачастую полагают, что обобщенные силы являются функциями обобщенных координат эквивалентной системы и их производных. Для упрощения задачи указанные функции разлагают в ряд Тейлора и используют только линейные части этих разложений. Иногда аналогичным способом находят только силы сопротивления почвы, считая их функциями ее механических характеристик и режимных параметров машин.
Такой метод является очень приближенным, поскольку не учитывает специфики процессов взаимодействия различных рабочих органов с почвой. Кроме того, в этом случае для уточнения аналитических зависимостей необходимо испытывать не отдельные рабочие органы, а макетные образцы машин, что ограничивает область использования полученных результатов.
Указанные недостатки относятся и к случаю использования экспериментальных записей сил. При существующих способах измерений в регистрируемых процессах взаимодействия рабочих органов с почвой содержится информация и о динамике самих рабочих органов [288], которая в значительной мере определяется конструкцией агрегата. Поэтому такую информацию можно отнести только к конкретному образцу агрегата, что не позволяет варьировать его параметры при моделировании.
в связи с изложенным целесообразно воспользоваться функциональными зависимостями, полученными методами механики почв, которые связывают силы сопротивления с механическими характеристиками почвы, геометрическими и режимными параметрами 1рабочих органов.
В механике почв силы сопротивления изучают на основе статических моделей, предполагающих неизменность условий взаимодействия и механических свойств почвы. Следовательно, найденные этими методами зависимости можно рассматривать как статические характеристики систем «почва — рабочий орган».
С целью выбора необходимых формул для определения сил сопротивления почвы проанализируем результаты исследовании различных авторов, посвященных этим вопросам.
Деформирование почвы при работе гладкого катка и качении колеса с жестким цилиндрическим ободом подчинено одинаковым закономерностям [435]. Это позволяет использовать для наших целей теорию качения колеса по деформируемой поверхности, основные положения которой разработаны в трудах акад. В. П. Го- рячкина, В. А. Желиговского и получили свое дальнейшее развитие в работах акад. М. Н. Летошнева, П. М. Василенко, профессора С. С. Саакяна и других ученых.
К настоящему времени предложено несколько зависимостей для определения сил сопротивления почвы, возникающих при качении колеса. Это формулы Гранвуане-Горячкина, В. В. Шульца, Герстнера, Бернштейна, М. Н. Летошнева, П. М. Василенко, Ю. А. Вейса и других авторов. Отличия этих формул обусловлены различными исходными посылками.
Так, акад. В. П. Горячкин при изучении качения колеса предполагал, что сминание почвы происходит по линиям ортогональным к окружности обода колеса [136] .В последующем акад. Б. А. Желиговским было установлено, что при учете сил трения смятие почвы не будет совпадать с направлением нормали к поверхности обода [170]. Поэтому модель процесса взаимодействия колеса с почвой акад. В. П. Горячкина отражает частный случай.
Зависимости, описывающие статическое качение колеса в общем случае, даны акад. П. М. Василенко [101], однако ввиду сложности практическое использование их весьма затруднено.
)Рассмотренные теории качения колеса базируются на представлении о почве как линейно деформируемой среде. Многочисленные исследования процесса сжатия почв, проведенные с помощью твердомеров, показали, что только в начальной фазе сжатия деформации растут пропорционально напряжениям. Поэтому для описания деформирования почвы сначала использовался степенной, а позднее гиперболический законы.
В общем случае для всего многобразия типов почв, их состояний и величин смятия гиперболический закон более точно отражает взаимосвязь напряжений и деформаций [220]. Для некоторых типов почв, при небольшой влажности, с экспериментальными результатами хорошо согласуется степенной закон. Поэтому целесообразность применения того или иного закона деформирования почвы зависит от конкретных почвенных условий и особенно от величины деформации.
По данным проф. С. С. Саакяна [413], для глубин вдавливания до 0,02 м почву можно рассматривать как линейно деформируемую среду.
Наблюдения за работой макетных образцов овощной сеялки показали, что глубина колеи опорных катков секций, как правило, не превышает 0,02—0,025 м. В связи с этим при определении сил сопротивления почвы, действующих на катки, за основу была принята формула Гранвуане—Горячкина, которая, как указывает Г. Н. Синеоков [435], является наиболее достоверной.
В соответствии с этой формулой выражения для проекций сил сопротивления на координатные оси имеют вид
где bk — ширина катка; δ1 — коэффициент объемного смятия почвы; h1 — глубина колеи.
Для учета влияния скорости движения катков была принята зависимость, аналогичная формуле Ю. К- Киртбая
где F' — деформационная составляющая силы сопротивления, определимая по формулам акад. В. П. Горячкина; f — коэффициент, учитывающий влияние скорости.
Тогда составляющие F,* и Fly сил сопротивления, действующих на катки сошниковой системы, можно представить в виде
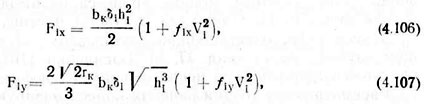
где V1 — скорость оси катка; fix, fiy — коэффициенты, учитывающие влияние скорости на соответствующие составляющие силы сопротивления.
При изучении взаимодействия сошников с почвой все исследователи, применяя метод акад. В. П. Горячкииа, расчленяли общее сопротивление на деформационную и динамическую составляющие, но использовали различные модели процесса взаимодействия.Сопоставляя экспериментальные данные ряда авторов можно заключить, что сила сопротивления зависит только от длины клиновидной части сошника, а длина щек практически не оказывает влияния. Так как длина клиновидной части килевидного сошника переменна и зависит от глубины хода, то можно считать, что
Поэтому для деформационной составляющей FE силы сопротивления почвы была выбрана формула
Динамическую составляющую силы сопротивления, вызванную отбрасыванием частиц почвы, большинство авторов принимают пропорциональной квадрату скорости
где fc — коэффициент, учитывающий влияние скорости; Vc — скорость движения сошника.
Используя зависимость (4.108) и формулу Ю. К. Киртбая [226], тяговое сопротивление сошника Fcx можно определить из выражения
Вертикальная составляющая силы сопротивления Fcy находится по известной формуле
где λ - угол наклона силы сопротивления к горизонту (считаем его постоянным).
Последовательное расположение рабочих органов у двухопорной сошниковой секции приводит к различиям условий их работы. Передний (уплотняющий) каток взаимодействует с почвой, поверхность уп и плотность р„ которой определяются предшествующей обработкой. После прохода уплотняющего катка изменяется плотность почвы и образуется новая поверхность. Степень уплотнения зависит от типа и влажности почвы, геометрических размеров, массы и скорости движения катка и прямо пропорциональна глубине колеи [195, 315].
В первом приближении можно принять, что плотность ρi почвы после прохода переднего катка равна
где Ψ' — коэффициент, учитывающий влияние формы, размеров катка, глубины его колеи и свойств почвы па ее уплотнение; h1 — глубина колеи переднего катка.
Сошник, двигаясь по следу уплотняющего катка, взаимодействует с почвой плотностью ρ0. Характер процесса бороздообразования при этом определяется состоянием почвы, геометрическими параметрами и режимом работы сошника.
При движении килевидного сошника в почве возникают различные зоны деформаций — уплотненная (нижние слои) и разрыхленная (верхние слои). В целом в зоне прохода сошника почва уплотняется незначительно (увеличение плотности не превышает 7%). С ростом скорости движения сошника степень уплотнения почвы уменьшается. Поэтому можно считать, что задний (прикатывающий) каток сошниковой секции взаимодействует с почвой той же плотности ρi, что и сошник.
Механические характеристики почвы зависят от ее плотности, причем такие, как твердость, коэффициент объемного смятия и удельное сопротивление с ней связаны линейно [67, 112].
В том случае, если коэффициент объемного смятия почвы, подготовленной к посеву, равен δо, то после прохода переднего катка он будет:
где δ1 — коэффициент объемного смятия почвы после прохода переднего катка; ψ1 — коэффициент, учитывающий влияние формы, размеров катка, глубины его колеи и свойств почвы.
Это значение коэффициента объемного смятия (6]) сохранится для почвы и после прохода сошника.
Коэффициент к связан линейной зависимостью с коэффициентом объемного смятия почвы Si
где kc — безразмерный коэффициент, учитывающий влияние формы деформатора.
Тогда
Горизонтальная составляющая F1x силы сопротивления, действующая на передний каток, с учетом формулы (4.106), равна
где V4 — проекция скорости оси переднего катка на ось ОХ.
Глубина колеи h1 определяется разностью ординат: точки АS обода катка уАS и профиля поля — уП
Как указывалось ранее, при изучении динамики сошниковой системы необходимо рассматривать профиль поверхности поля, и твердость почвы как случайные функции времени (или пути), т. е.
Выразив ординату уАS через параметры сошниковой системы и обобщенные координаты, найдем глубину колеи переднего катка
Принимая для простоты 
и подставив зависимость (4.114) в формулу (4.113), получим выражение для F1х
Аналогично находится и вертикальная составляющая F1y силы сопротивления почвы
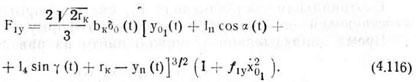
Тяговое сопротивление сошника с учетом выражений (4.109) и (4.112) имеет вид
где δ1с — коэффициент объемного смятия почвы для сошника. Формула (4.116) получена в предположении, что 
У двухопорной сошниковой секции сошник с запаздыванием проходит любую точку поверхности поля по сравнению с уплотняющим катком. Поэтому глубина хода сошника hс определяется разностью ординат уА7 и уА8 взятых в различные моменты времени
где уА7 — ордината для бороздки, образованного пяткой сошника; уА8 — ордината поверхности, образованной передним катком; τ1 — время запаздывания сошника.
Выразим ординаты уА7 и уА8 через обобщенные координаты и параметры сошниковой системы, тогда глубина хода сошника будет равна
где l7, d2 — горизонтальная и вертикальная координаты точки А7 и системе отсчета X2O2Y2.
Коэффициент объемного смятия почвы δ1с определяется по формуле (4.111) и с учетом запаздывания равен
Подставив в формулу (4,117) зависимости (4.118) и (4.119), получим выражение для тягового сопротивления сошника
Вертикальная составляющая Fcy силы сопротивления почвы, действующей на сошник, находится по формуле (4.110). Время запаздывания τ1 можно найти из равенства.
Выразив абсциссы xA8 и хA7 через параметры сошниковой системы и ее обобщенные координаты и произведя необходимые преобразования, получим уравнение для τ1
Из этого уравнения τ1 находим методом последовательных приближений. При этом в качестве начального значения τ1 можно принять величину τ1
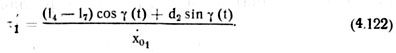
Выражение для силы сопротивления качению заднего (прикатывающего) катка имеет вид
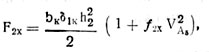
где h2 — глубина колеи заднего катка; VA5 — проекция скорости оси вращения катка на ось ОХ; δ1K — коэффициент объемного смятия почвы для заднего катка/.
Глубину колеи h2 можно определить по разности ординат поверхностей, формируемых проходами сошника и прикатывающего катка.
Рассмотрим процесс образования этих поверхностей. При посеве сошник своим килем раздвигает почву, вытесняя ее на дневную поверхность. После прохода сошника осыпается только часть почвы и образуется остаточная бороздка с небольшими почвенными валиками по бокам, которые, имея небольшую твердость, практически без сопротивления сминаются прикатывающим катком. При этом происходит перераспределение почвы — остаточная бороздка закрывается и поверхность выравнивается, приближаясь к поверхности, созданной уплотняющим катком. Аналогичная картина наблюдается и при работе сошниковой секции с загортачами.
Поэтому отсчет глубины колеи h2 заднего катка можно производить от траектории движения обода переднего катка
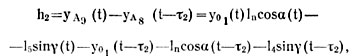
где τ2 — время запаздывания заднего катка по сравнению с передним.
Коэффициент объемного смятия почвы δ1K ( для прикатывающего катка определяется по формуле (4.111). С учетом запаздывания он равен
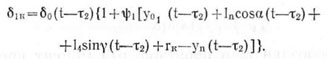
Если принять 
горизонтальная, F2х и вертикальная F2y, составляющие силы сопротивления почвы, действующей на задний каток, будут равны соответственно
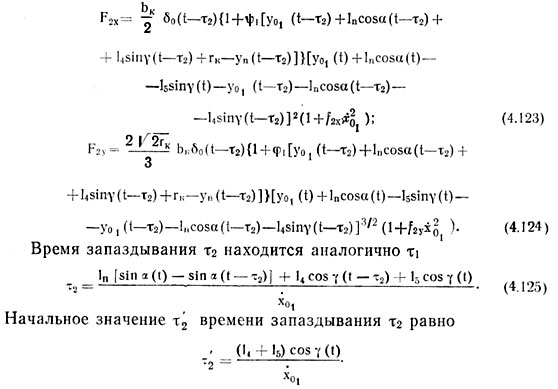
Рис. 4.16. К определению силы давления нажимной пружины.
Будем считать, что при α = α0 ось пружиныперпендикулярна поводку. Для произвольного положения поводка можно записать
где Fnp — усилие предварительного сжатия пружины; С — жесткость пружины; Δ — деформация пружины.
Как следует из рис. 4.16, деформация пружины равна
Учитывая, что
Глубина бороздки hs в произвольный момент времени определяется разностью ординат траекторий движения пятки сошника (точки А7) и обода прикатывающего катка (точки А9)
где τ3 — время запаздывания заднего катка по сравнению с сошником.
Подставив в это выражение значения ординат уА7 и уА9 найдем зависимость, связывающую глубину бороздки с параметрами сошниковой системы
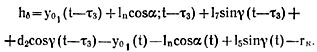
Время запаздывания τ3 и его начальное значение τ3 можно определить по формулам
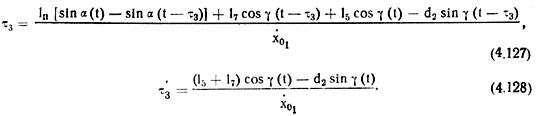
Дифференциальные уравнения (4.103) совместно с зависимостями (4.80), (4.81), (4.U0), (4.115), (4.120), (4.123), (4.124) и (4.126) образуют замкнутую систему. Для ее решения, т. е. отыскания законов изменения обобщенных координат 
необходимо задать начальные условия, которые для данного случая имеют вид
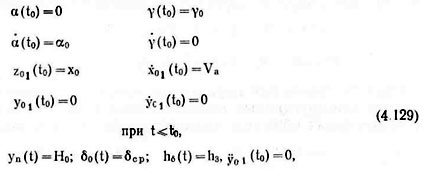
где Va — скорость посевного агрегата; δср — среднее значение коэффициента объемного смятия почвы, подготовленной к посеву; h3 — заданная глубина посева семян.
Начальные значения обобщенных координат находятся из уравнений статики
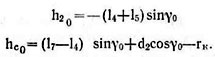
Поскольку поверхность поля является односторонней связью, то на силы сопротивления накладываются ограничения
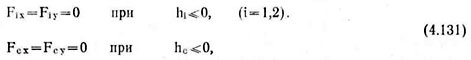
Области изменения параметров сошниковой системы выбраны с учетом конструктивных возможностей и опыта эксплуатации экспериментальных образцов овощной сеялки точного высева
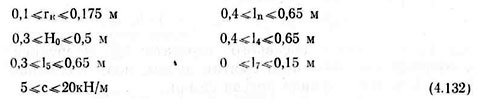
Одним из основных показателей качества работы сошниковой системы является стабильность глубины борозды hδ (глубины заделки семян). Поэтому будет естественным выбрать в качестве критерия оптимальности минимум дисперсии этой величины
где hδср — среднее значение глубины бороздки.
Вычислив дисперсию hs для различных вариантов параметров сошниковой секции путем многократного численного интегрирования на ЭВМ системы дифференциальных уравнений (4.103) {например, методом Эйлера, Пикара, Рунге-Кутта и др.), найдем функцию:
где рi — параметр сошниковой секции (i = l, 2, ..., n).
В связи с наличием прямых ограничений на область допустимых значений параметров вида
(где 
— предельные значения данного параметра) определение их оптимальных величин формально сводится к отысканию глобального условного экстремума функции 
одним из известных методов (например, методом возможных направлений, условного градиента, штрафных функций и др.). Представляет практический интерес получение простой аналитической зависимости дисперсии глубины бороздки, которая могла бы быть использована при проектировании аналогичных сошниковых систем без решения дифференциальных уравнений (4.103).
В этом случае сначала находится значение функции на некотором дискретном множестве точек 
, а затем по методу наименьших квадратов для нее ищется приближение в виде полинома порядка v<n (где п — число основных параметров сошниковой системы)
где Ci — коэффициенты.
Для сокращения объема вычислений при выборе точек 
можно воспользоваться методами теории планирования эксперимента.
ДДоставка сельхозтехники и запасных частей, оросительных систем, насосов во все города России (быстрой почтой и транспортными компаниями), так же через дилерскую сеть: Москва, Владимир, Санкт-Петербург, Саранск, Калуга, Белгород, Брянск, Орел, Курск, Тамбов, Новосибирск, Челябинск, Томск, Омск, Екатеринбург, Ростов-на-Дону, Нижний Новгород, Уфа, Казань, Самара, Пермь, Хабаровск, Волгоград, Иркутск, Красноярск, Новокузнецк, Липецк, Башкирия, Ставрополь, Воронеж, Тюмень, Саратов, Уфа, Татарстан, Оренбург, Краснодар, Кемерово, Тольятти, Рязань, Ижевск, Пенза, Ульяновск, Набережные Челны, Ярославль, Астрахань, Барнаул, Владивосток, Грозный (Чечня), Тула, Крым, Севастополь, Симферополь, в страны СНГ:Киргизия, Казахстан, Узбекистан, Киргизстан, Туркменистан, Ташкент, Азербайджан, Таджикистан.
