Распределение семян сеялками для рядового и полосового посевов
Обычный рядовой посев семян овощных культур проводится преимущественно сеялками с катушечными высевающими аппаратами. Согласно многочисленным исследованиям, они имеют ряд существенных недостатков, к числу которых следует отнести, прежде всего, большую неравномерность подачи мелких семян, особенно при посеве с малыми нормами высева. Объясняется это тем, что таким аппаратам свойственны два вида движения зернового потока: принудительное, создаваемое желобками рабочей катушки, и активное, вызываемое наличием послойного трения между семенами. Желобки катушки создают порционность высева, а движение «активного слоя» сопровождается привходящими факторами (микроподъемы, повороты семян, частичная замена трения скольжения трением качения и др.), обусловливающими случайный характер количественной подачи семян.
В конечном счете катушечный высевающий аппарат создает такой общий поток семян, в котором невозможно хотя бы приближенно выделить исходные интервалы между подачами семян, т. е. невозможно аналитически выявить зависимость величины исходных интервалов между семенами от каких-то наперед заданных кинематических или геометрических параметров высевающей системы. Поэтому анализ распределения семян при рядовом и полосовом посевах можно вести только методами теории вероятностей и математической статистики.
Учитывая, что обычный рядовой посев предполагает наличие конечных интервалов между семенами, для аналитических целей можно воспользоваться разделом теории случайных функций — теорией потоков случайных событий.
В общем комплексе потоков случайных событий процесс распределения семян принадлежит к простейшему (Пуассоновскому) потоку, так как он обладает всеми свойствами, характерными для этого вида потока, а именно: стационарностью, ординарностью и отсутствием последействия.
Свойство стационарности процесса распределения как потока случайных событий вытекает из того, что в практике посева йоли- чество семян, располагающихся на участке рядка, зависит от длины этого участка и не зависит от того, на каком именно рядке засеянного поля он выбран. С математической стороны это означает, что вероятность попадания того или иного количества семян на участок рядка определенной длины зависит только от длины этого участка и не зависит от того, где именно выбран этот участок.
Ординарность процесса распределения семян означает пренебрежительно малую вероятность попадания двух и более семян на элементарный участок длины рядка, по сравнению с вероятностью попадания на этот участок одного семени.
Что касается третьего свойства простейшего потока, то процесс распределения семян как процесс образования интервалов между ними в действительности им не обладает, так как величина интервалов между семенами определяется положением предыдущего и последующего семени. Однако, если учесть, что при рядовом посеве, вследствие малости промежутка времени между выбрасыванием семян высевающим аппаратом, возникает значительное количество инверсий, то для упрощения анализа можно без особой погрешности пренебречь наличием последействия.
Распределение семян, как случайный процесс, обладает эргодическим свойством, которое состоит в том, что каждая реализация случайного процесса (засеянный рядок) достаточной протяженности является характеристикой всей совокупности возможных реализаций (всего поля в целом). Это свойство было использовано при экспериментальном анализе процесса распределения семян и растений в лабораторных и полевых условиях.
Вероятность того, что на элементарный отрезок попадает одно семя, т. е. отрезок будет «занят», равна 
вероятность того, что он окажется «пустым», равна 
. Так как попадание семян на элементарный участок, в силу допущения об отсутствии последействия,, независимо, то попадание или непопадание семян п отрезков можно рассматривать как результаты п независимых опытов. По теореме о повторении опытов, вероятность того, что среди общего числа п отрезков будет m «занятых» семенами, равна
Рис. 4.18. Схема к выводу уравнения распределения промежутков между семенами при обычном.
При достаточно большом числе отрезков п эту вероятность можно приближенно считать искомой вероятностью (Рm) попадания m семян на отрезок рядка 1. Чтобы найти Рm, перейдем в выражении (4.134) к пределу при n → ∞.
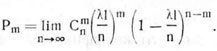
Преобразование выражения под знаком предела дает:
Входящая в формулу (4.135) величина λ1 есть среднее число семян, высеянных на длине рядка 1 (математическое ожидание числа семян, попавших на этот участок).
Распределение случайной величины, характеризуемое формулой (4.135), является распределением (законом) Пуассона с параметром к.
Для определения закона распределения интервалов между семенами рассмотрим случайную величину Т промежутка между двумя соседними произвольными событиями (семенами) в простейшем потоке (рис. 4.18) и найдем функцию ее распределения
или, переходя к вероятности противоположного события, имеем
Вероятность того, что на участок рядка длиной t, начинающийся в момент тш появления одного из семян, не упадет пи одно из последующих семян, можно вычислить по формуле (4.135) при т — 0, если учесть ранее сделанное допущение об отсутствии последействия
Дифференцируя это уравнение, определим плотность распределения
Закон распределения с плотностью (4.137) является показательным. В соответствии с этим, числовые характеристики расстояний (интервалов) между семенами при рядовом посеве определятся из выражении
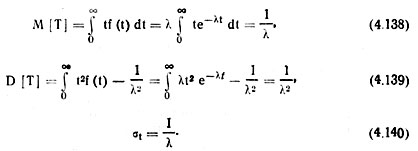
Нетрудно убедиться, что коэффициент вариации интервалов между семенами для этого способа посева равен 100%.
Таким образом, распределение интервалов между семенами при обычном рядовом посеве подчиняется показательному закону.
При полосовом способе посева семена, как известно, распределяются не узкими рядками, а полосами шириной 0,1—0,12 м. Применяемые для этой цели сошники со специальными распределителями семян обеспечивают сравнительно равномерное их размещение по ширине полосы. Если разбить полосу вдоль ее длины на п частей, то каждую такую часть можно рассматривать как отдельный рядок, аналогичный рядку рядового посева.
Семена в каждом рядке полосы в соответствии с предпосылками, сделанными выше, размещаются случайно. Поэтому процесс распределения семян в рядке полосы можно представить как поток событий, обладающий стационарностью и ординарностью, а процесс распределения семян при этом способе посева — как сумму потоков.
Рис. 4.19. Схема к выводу уравнения распределения семян при полосовом посеве.
Последействие в каждом отдельном потоке (в каждом отдельном рядке полоски) может быть значительным ввиду малости значений параметра % (имеется в виду, что норма высева семян при полосовом посеве такая же, как и при рядовом). Однако установлено [111], что при суммировании (взаимном наложении) большого числа ординарных стационарных потоков с практически любым последействием получается поток, близкий к простейшему.
Следовательно, процесс распределения семян при полосовом посеве можно рассматривать как простейший поток случайных событий. Условия, которые должны при этом соблюдаться, аналогичны условиям центральной предельной теоремы, а именно: складываемые потоки должны оказывать на их сумму равномерно малое влияние. Соблюдение этого условия в нашем случае обеспечивается равномерным распределением семян по ширине полоски, т. е. примерно равными значениями параметров потоков, отвечающих каждому рядку полосы.
Пусть каждому рядку полосы, полученному делением ее на п равных частей, отвечают соответственно потоки П1, П2, П3, П4, ..., Пn. «Суммирование» этих потоков состоит в том, что все моменты появления событий сносятся на одну и ту же ось (рис. 4.19). Рассмотрим суммарный поток 
на оси ot. Очевидно, что поток П должен быть стационарным и ординарным, так как каждое слагаемое обладает этим свойством и они независимы. Кроме того, можно предположить, что при увеличении числа слагаемых последействие в суммарном потоке, даже если оно значительно в отдельных потоках, должно постепенно слабеть. Действительно, рассмотрим на оси ot два неперекрывающихся отрезка T1 и Т2. Каждое семя, попадающее в эти отрезки, случайным образом может оказаться принадлежащим тому или иному потоку и, по мере увеличения п, удельный вес семян, принадлежащих одному и тому же потоку, должен уменьшаться, остальные же семена принадлежат разным потокам и появляются на отрезках T1 и Т2 независимо друг от друга. Естественно ожидать, что при увеличении и в суммарном потоке будет ослабевать последействие и он будет приближаться к простейшему.
На практике [111] оказывается достаточным сложить 4—5 потоков, чтобы получить суммарный поток, с которым можно оперировать, как с простейшим.
Произведя вычисления для суммарного потока, аналогичные изложенным выше, получим необходимые данные, характеризующие процесс распределения семян при полосовом посеве
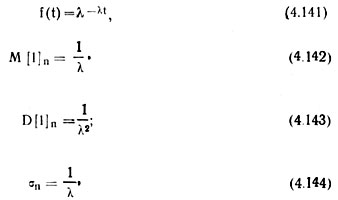
где f(t) — плотность интервалов между семенами; М [l]n — математическое ожидание интервалов между семенами; D [1]n, σn — соответственно дисперсия и квадратическое отклонение интервалов между семенами; λ — среднее количество семян, высеваемых на единицу длины полосы.
Следовательно, распределение интервалов между семенами в направлении длины полосы при полосовом посеве, так же, как и при рядовом, подчиняется показательному закону. Отсюда видно, что при одинаковой норме высева семян или, что то же, при одинаковой плотности потока {%), распределение интервалов между семенами вдоль рядка (полосы) при рядовом и полосовом посевах будет одинаковым. Но если учесть, что при полосовом посеве, благодаря рассредоточенному размещению семян, создается возможность выращивания значительно большего количества растений, а следовательно, и возможность применения большей нормы высева, то, согласно выражению (4.143), дисперсия интервалов между семенами при полосовом посеве будет значительно меньше дисперсии при обычном рядовом.
Например, при возделывании моркови на средних по плодородию почвах оптимальное количество растений на погонной длине рядка в 1 метр обычного рядового посева принимается равным примерно 50 шт. При полосовом посеве число растений увеличивают до 70 шт. Если принять, что абсолютная полевая всхожесть семян в этом случае равна 0,25, то при рядовом посеве на погонной длине 1 метр рядка нужно высевать 200 шт. семян, а при полосовом — 280 шт. Дисперсия интервалов между семенами при рядовом посеве составит 0,25 см, а при полосовом — 0,125 см, т. е. при оговоренных условиях дисперсия интервалов полосового посева в два раза меньше, чем при обычном рядовом.
Отсюда следует, что полосовой посев, кроме общепризнанных достоинств (не требуется прорывка всходов, лучшая поперечная равномерность распределения семян), имеет также существенное преимущество перед рядовым в отношении продольной равномерности распределения семян, что обеспечивает повышение урожайности высеваемой культуры.
ДДоставка сельхозтехники и запасных частей, оросительных систем, насосов во все города России (быстрой почтой и транспортными компаниями), так же через дилерскую сеть: Москва, Владимир, Санкт-Петербург, Саранск, Калуга, Белгород, Брянск, Орел, Курск, Тамбов, Новосибирск, Челябинск, Томск, Омск, Екатеринбург, Ростов-на-Дону, Нижний Новгород, Уфа, Казань, Самара, Пермь, Хабаровск, Волгоград, Иркутск, Красноярск, Новокузнецк, Липецк, Башкирия, Ставрополь, Воронеж, Тюмень, Саратов, Уфа, Татарстан, Оренбург, Краснодар, Кемерово, Тольятти, Рязань, Ижевск, Пенза, Ульяновск, Набережные Челны, Ярославль, Астрахань, Барнаул, Владивосток, Грозный (Чечня), Тула, Крым, Севастополь, Симферополь, в страны СНГ:Киргизия, Казахстан, Узбекистан, Киргизстан, Туркменистан, Ташкент, Азербайджан, Таджикистан.
